Пожалуй, эту статью нельзя назвать самой востребованной, но мне она показалось интересной, поэтому я решил её написать. Не то, чтобы я рекомендую делать так, как описано в статье, скорей мне хочется продемонстрировать некоторые вещи, касающиеся создания 3D-моделей в WebGL.

Однажды меня кто-то спросил, как сделать модель кегли для боулинга в WebGL. Правильным ответом было бы "Используйте программу для 3D-моделирования, наподобие Blender, Maya, 3D Studio Max, Cinema 4D и т.д.". Используйте её для моделирования кегли, затем экспортируйте модель и загрузите её в своём приложении. (Относительно простым форматом является OBJ).

Но спустя некоторое время я подумал - а что, если человеку нужно было сделать собственную библиотеку для моделирования?

У меня появилось несколько идей. Одна из них - сделать цилиндр, а затем сузить его в нужных местах через синусоиду. Проблема в том, что вы не получите необходимой плавности в верхней части. Обычный цилиндр состоит из нескольких равноудалённых колец, но в местах изгибов необходимо больше колец, чтобы достичь нужной плавности.

В пакете для моделирования вы бы начали с создания двумерного силуэта, точнее с кривой линии, соответствующей грани двумерного силуэта. А затем создали 3D-объект на основе силуэта. Этого можно достичь, вращая силуэт вокруг определённой оси, создавая в процессе вращения точки фигуры. Эта техника позволяет легко создать любой закруглённый объект вроде шара, стакана, бейсбольной биты, бутылки, лампочки и т.д.

Как же нам сделать это? Для начала нужно получить кривую. Затем нам необходимо получить точки этой кривой. Затем, вращая эти точки вокруг какой-то оси с помощью математики матриц, мы построим треугольники.

Самой распространённой кривой в компьютерной графике, похоже, является кривая Безье. Если вы когда-либо редактировали кривую в Adobe Illustrator, или Inkscape, или Affinity Designer, или в других похожих программах, то вы имели дело с кривой Безье.

Кривая Безье (кубическая кривая Безье, если быть точным) формируется на основе 4 точек - 2 конечные точки и 2 "контрольные точки".

Вот эти 4 точки:

Возьмём число между 0 и 1 (назовём его t), где 0 = начало, а 1 - конец. Затем вычислим соответствующие точки t между каждой парой точек P1 P2, P2 P3, P3 P4.

Другими словами, при t = .25, вы вычислим 25% пути от точки P1 до P2, затем 25% пути от точки P2 до P3 и, наконец, 25% пути от точки P3 до P4.

Потяните за слайдер для регулировки t, также с помощью мыши можно перемещать точки P1, P2, P3 и P4.

Далее проделаем то же самое для полученных точек - вычислим t между точками Q1 Q2 и Q2 Q3.

Наконец, находим t для точек R1 R2.

Положение красной точки задаёт кривую.

Это и есть кубическая кривая Безье.

Стоит заметить, что хотя описанная выше интерполяция по созданию 3 точек из 4, затем 2 точек из 3 и, наконец, одной точки из 2 делает своё дело, такой подход нельзя назвать общепринятым. Вместо этого кто-то разобрался во всей математике и упростил всё до следующей формулы:

invT = (1 - t)
P = P1 * invT^3 +
    P2 * 3 * t * invT^2 +
    P3 * 3 * invT * t^2 +
    P4 * t^3

где P1, P2, P3, P4 - точки из примера выше, а P - красная точка.

В программах по работе с векторными 2D-изображения вроде Adobe Illustrator при создании более длинных кривых на самом деле создаётся несколько маленьких кривых из 4 точек, рассмотренных нами выше. По умолчанию большинство программ фиксируют контрольные точки вокруг общих начальной и конечной точки так, чтобы контрольные точки всегда были противоположны друг другу относительно общей точки.

На следующем примере при перемещении P3 или P5 противоположная им точка будет также смещаться.

Заметьте, что кривая P1,P2,P3,P4 - это самостоятельная кривая, как и кривая P4,P5,P6,P7. Именно когда P3 и P5 находятся на строго противоположных сторонах от P4, они выглядят как непрерывная кривая. Большинство приложений позволяют открепить P3 и P5 друг от друга и позволять таким образом создавать острые углы. Снимите пометку закрепления точек и потяните за P3 или P5, тогда станет очевидно, что перед нами две отдельные кривые.

Далее нам необходимо каким-то образом создать точки по нашей кривой. По формуле выше мы можем создать точку для значения t следующим образом:

function getPointOnBezierCurve(points, offset, t) {
  const invT = (1 - t);
  return v2.add(v2.mult(points[offset + 0], invT * invT * invT),
                v2.mult(points[offset + 1], 3 * t * invT * invT),
                v2.mult(points[offset + 2], 3 * invT * t * t),
                v2.mult(points[offset + 3], t * t * t));
}

Тогда мы сможем создать набор точек кривой:

function getPointsOnBezierCurve(points, offset, numPoints) {
  const points = [];
  for (let i = 0; i < numPoints; ++i) {
    const t = i / (numPoints - 1);
    points.push(getPointOnBezierCurve(points, offset, t));
  }
  return points;
}

Обратите внимание, что я добавил небольшие функции-помощники JavaScript v2.mult и v2.add для упрощения работы с точками.

Вы можете выбрать количество точек на приведённой диаграмме. Для резких изгибов понадобится больше точек. Если же кривая больше напоминает ровную линию, можно использовать меньше точек. Одно из решений - проверять, насколько кривая кривая. Если линия слишком кривая, можно разбить её на две части.

Разбить кривую совсем несложно. Если снова взглянуть на разные уровни интерполяции, точки P1, Q1, R1 и КРАСНАЯ точка составляют одну кривую, а точки КРАСНАЯ, R2, Q3, P4 образуют вторую кривую для любого значения t. Другими словами, мы в любом месте можем разбить одну кривую и получить из неё две кривых.

Теперь нам осталось решить, нужно ли разделять кривую или нет. Посмотрев по интернету я нашёл функцию, которая определяет, насколько ровная наша кривая линия.

function flatness(points, offset) {
  const p1 = points[offset + 0];
  const p2 = points[offset + 1];
  const p3 = points[offset + 2];
  const p4 = points[offset + 3];

  let ux = 3 * p2[0] - 2 * p1[0] - p4[0]; ux *= ux;
  let uy = 3 * p2[1] - 2 * p1[1] - p4[1]; uy *= uy;
  let vx = 3 * p3[0] - 2 * p4[0] - p1[0]; vx *= vx;
  let vy = 3 * p3[1] - 2 * p4[1] - p1[1]; vy *= vy;

  if(ux < vx) {
    ux = vx;
  }

  if(uy < vy) {
    uy = vy;
  }

  return ux + uy;
}

Можно использовать определение ровности в нашей функции, которая создаёт точки кривой. Для начала проверим, сильно ли отличается от прямой линии наша кривая. Если сильно, мы будем разбивать на несколько линий, иначе просто добавим точки в массив.

function getPointsOnBezierCurveWithSplitting(points, offset, tolerance, newPoints) {
  const outPoints = newPoints || [];
  if (flatness(points, offset) < tolerance) {

    // кривизна в пределах допустимого, просто добавим точки кривой
    outPoints.push(points[offset + 0]);
    outPoints.push(points[offset + 3]);

  } else {

    // кривизна больше заданного порога, разбиваем
    const t = .5;
    const p1 = points[offset + 0];
    const p2 = points[offset + 1];
    const p3 = points[offset + 2];
    const p4 = points[offset + 3];

    const q1 = v2.lerp(p1, p2, t);
    const q2 = v2.lerp(p2, p3, t);
    const q3 = v2.lerp(p3, p4, t);

    const r1 = v2.lerp(q1, q2, t);
    const r2 = v2.lerp(q2, q3, t);

    const red = v2.lerp(r1, r2, t);

    // первая половина
    getPointsOnBezierCurveWithSplitting([p1, q1, r1, red], 0, tolerance, outPoints);
    // вторая половина
    getPointsOnBezierCurveWithSplitting([red, r2, q3, p4], 0, tolerance, outPoints);

  }
  return outPoints;
}

С этим алгоритмом мы можем быть уверены, что у нас будет достаточно точек, однако, алгоритм не заботится о том, что получатся лишние точки.

Для этого нам поможет другой алгоритм, который я также нашёл на просторах сети - алгоритм Рамера-Дугласа-Пекера

Итак, у нас есть массив точек. Мы находим точку на кривой, максимально удалённую от отрезка, соединяющего первую и последнюю точку кривой. Потом мы сравниваем расстояние от отрезка до этой точки с условным значением. Если полученное расстояние меньше этого условного значения, мы просто оставляем 2 конечные точки, а все остальные точки исключаем. Иначе мы снова запускаем алгоритм - один раз на линии, начинающейся с первой точки и заканчивающейся на максимально удалённой точке, а второй раз запускаем на линии, начинающейся на максимально удалённой точке и заканчивающейся на последней точке кривой.

function simplifyPoints(points, start, end, epsilon, newPoints) {
  const outPoints = newPoints || [];

  // находим максимально удалённую точку от отрезка, соединяющего конечные точки
  const s = points[start];
  const e = points[end - 1];
  let maxDistSq = 0;
  let maxNdx = 1;
  for (let i = start + 1; i < end - 1; ++i) {
    const distSq = v2.distanceToSegmentSq(points[i], s, e);
    if (distSq > maxDistSq) {
      maxDistSq = distSq;
      maxNdx = i;
    }
  }

  // если точка слишком далеко
  if (Math.sqrt(maxDistSq) > epsilon) {

    // разделяем
    simplifyPoints(points, start, maxNdx + 1, epsilon, outPoints);
    simplifyPoints(points, maxNdx, end, epsilon, outPoints);

  } else {

    // иначе оставляем конечные точки
    outPoints.push(s, e);
  }

  return outPoints;
}

Функция v2.distanceToSegmentSq вычисляет квадратично расстояние от точки до отрезка. Мы используем квадратичное расстояние, так как его проще вычислить по сравнению с настоящим расстоянием. Для получения самой отдалённой от отрезка точки квадратичного расстояния нам вполне достаточно.

Ниже идёт демонстрация. Регулируя расстояние, можно наблюдать, как добавляются или удаляются точки.

Вернёмся к нашей кегле. Мы могли бы сделать полноценный редактор на основе приведённого выше кода. Редактор, который бы мог добавлять и удалять точки, закреплять и откреплять контрольные точки, выполнять действие назад и так далее... Но есть способ попроще. Мы можем просто взять один из зрелых редакторов, упомянутых выше. Я использовал этот онлайн-редактор.

Вот такой контур кегли у меня получился:

Контур состоит из 4 кривых Безье. Данные для этой кривой выглядят следующим образом:

<path fill="none" stroke-width="5" d="
   m44,434
   c18,-33 19,-66 15,-111
   c-4,-45 -37,-104 -39,-132
   c-2,-28 11,-51 16,-81
   c5,-30 3,-63 -36,-63
"/>

Интерпретируя данные, мы получим точки.

        ___
44, 371,   |
62, 338,   | 1-я кривая
63, 305,___|__
59, 260,___|  |
55, 215,      | 2-я кривая
22, 156,______|__
20, 128,______|  |
18, 100,         | 3-я кривая
31,  77,_________|__
36,  47,_________|  |
41,  17,            | 4-я кривая
39, -16,            |
 0, -16,____________|

Итак, у нас есть данные для кривых, теперь нам нужно вычислить точки для них.

// получаем точки вдоль всех сегментов
function getPointsOnBezierCurves(points, tolerance) {
  const newPoints = [];
  const numSegments = (points.length - 1) / 3;
  for (let i = 0; i < numSegments; ++i) {
    const offset = i * 3;
    getPointsOnBezierCurveWithSplitting(points, offset, tolerance, newPoints);
  }
  return newPoints;
}

Полученные точки не помешает прорядить функцией simplifyPoints.

Теперь нужно провернуть наши точки вокруг оси кегли. Мы определяем, из скольких частей будет состоять кегля, и для каждой части создаём точки, поворачивая исходную кривую вокруг оси Y, используя математику матриц. Когда все точки созданы, мы соединяем их треугольниками, используя индексы.

// поворот вокруг оси Y
function lathePoints(points,
                     startAngle,   // начальный угол (равен 0)
                     endAngle,     // конечный угол (равен Math.PI * 2)
                     numDivisions, // сколько частей будет создано при вращении
                     capStart,     // true, чтобы замыкать начальные точки
                     capEnd) {     // true, чтобы замыкать конечные точки
  const positions = [];
  const texcoords = [];
  const indices = [];

  const vOffset = capStart ? 1 : 0;
  const pointsPerColumn = points.length + vOffset + (capEnd ? 1 : 0);
  const quadsDown = pointsPerColumn - 1;

  // создание точек
  for (let division = 0; division <= numDivisions; ++division) {
    const u = division / numDivisions;
    const angle = lerp(startAngle, endAngle, u) % (Math.PI * 2);
    const mat = m4.yRotation(angle);
    if (capStart) {
      // добавляем начальные точки по оси Y
      positions.push(0, points[0][1], 0);
      texcoords.push(u, 0);
    }
    points.forEach((p, ndx) => {
      const tp = m4.transformPoint(mat, [...p, 0]);
      positions.push(tp[0], tp[1], tp[2]);
      const v = (ndx + vOffset) / quadsDown;
      texcoords.push(u, v);
    });
    if (capEnd) {
      // добавляем конечные точки по оси Y
      positions.push(0, points[points.length - 1][1], 0);
      texcoords.push(u, 1);
    }
  }

  // создаём индексы
  for (let division = 0; division < numDivisions; ++division) {
    const column1Offset = division * pointsPerColumn;
    const column2Offset = column1Offset + pointsPerColumn;
    for (let quad = 0; quad < quadsDown; ++quad) {
      indices.push(column1Offset + quad, column2Offset + quad, column1Offset + quad + 1);
      indices.push(column1Offset + quad + 1, column2Offset + quad, column2Offset + quad + 1);
    }
  }

  return {
    position: positions,
    texcoord: texcoords,
    indices: indices,
  };
}

Приведённый код создаёт координаты и текстурные координаты, затем создаёт индексы для дальнейшего создания из них треугольников. Переменные capStart и capEnd отвечают за создание замыкающих точек. Представьте, что мы бы создавали жестяную банку. Эти параметры указывали бы, нужно ли создавать дно и крышку.

Используя наш упрощённый код, на основании этих данных мы создаём буферы WebGL:

const tolerance = 0.15;
const distance = .4;
const divisions = 16;
const startAngle = 0;
const endAngle = Math.PI * 2;
const capStart = true;
const capEnd = true;

const tempPoints = getPointsOnBezierCurves(curvePoints, tolerance);
const points = simplifyPoints(tempPoints, 0, tempPoints.length, distance);
const arrays = lathePoints(points, startAngle, endAngle, divisions, capStart, capEnd);
const extents = getExtents(arrays.position);
if (!bufferInfo) {
  bufferInfo = webglUtils.createBufferInfoFromArrays(gl, arrays);

Вот, что у нас получилось:

Проверьте, как изменится результат, если изменить положение слайдеров.

Однако, здесь есть проблема. Включите галку "triangles" и вы заметите, что текстура наложена неравномерно. Причина в том, что текстурная координата v основана на индексе точек кривой линии. Если бы они были расположены равномерно по кривой, всё могло бы получиться. Теперь же нам придётся придумать что-то ещё.

Например, можно пройтись по точкам, вычислить общую длину кривой и расстояние до каждой точки на этой кривой. Затем делением на длину мы можем получить более подходящее значение для v.

// поворот вокруг оси Y
function lathePoints(points,
                     startAngle,   // начальный угол (равен 0)
                     endAngle,     // конечный угол (равен Math.PI * 2)
                     numDivisions, // сколько частей будет создано при вращении
                     capStart,     // true, чтобы замыкать начальные точки
                     capEnd) {     // true, чтобы замыкать конечные точки
  const positions = [];
  const texcoords = [];
  const indices = [];

  const vOffset = capStart ? 1 : 0;
  const pointsPerColumn = points.length + vOffset + (capEnd ? 1 : 0);
  const quadsDown = pointsPerColumn - 1;

+  // создаём v-координаты
+  let vcoords = [];
+
+  // вычисляем общую длину и расстояние до каждой точки
+  let length = 0;
+  for (let i = 0; i < points.length - 1; ++i) {
+    vcoords.push(length);
+    length += v2.distance(points[i], points[i + 1]);
+  }
+  vcoords.push(length);  // последняя точка
+
+  // делим каждое расстояние на общую длину
+  vcoords = vcoords.map(v => v / length);

  // создание точек
  for (let division = 0; division <= numDivisions; ++division) {
    const u = division / numDivisions;
    const angle = lerp(startAngle, endAngle, u) % (Math.PI * 2);
    const mat = m4.yRotation(angle);
    if (capStart) {
      // добавляем начальные точки по оси Y
      positions.push(0, points[0][1], 0);
      texcoords.push(u, 0);
    }
    points.forEach((p, ndx) => {
      const tp = m4.transformPoint(mat, [...p, 0]);
      positions.push(tp[0], tp[1], tp[2]);
*      texcoords.push(u, vcoords[ndx]);
    });
    if (capEnd) {
      // добавляем конечные точки по оси Y
      positions.push(0, points[points.length - 1][1], 0);
      texcoords.push(u, 1);
    }
  }

  // создаём индексы
  for (let division = 0; division < numDivisions; ++division) {
    const column1Offset = division * pointsPerColumn;
    const column2Offset = column1Offset + pointsPerColumn;
    for (let quad = 0; quad < quadsDown; ++quad) {
      indices.push(column1Offset + quad, column1Offset + quad + 1, column2Offset + quad);
      indices.push(column1Offset + quad + 1, column2Offset + quad + 1, column2Offset + quad);
    }
  }

  return {
    position: positions,
    texcoord: texcoords,
    indices: indices,
  };
}

Получилось получше

Но текстурные координаты по-прежнему не идеальны. Мы не решили, что делать с закрывающими точками. Это ещё одна причина, почему вам следует использовать программу для моделирования. Мы могли бы пробовать разные идеи для вычисления uv-координат для закрывающих точек, но вряд ли они нам сильно помогли. Если вы поищете текстурную карту бочки, вы увидите, что получение идеальных UV-координат не столько математическая проблема, сколько проблема входных данных, и вам понадобится хороший инструмент для задания этих данных.

Итак, идём дальше. До этого времени мы выпускали из виду одну вещь - это нормали.

Мы могли бы вычислить нормаль для каждой точки кривой. На самом деле, если вернуться к рассмотренным выше примерам, мы увидим, что линия между точками R1 и R2 является касательной к кривой.

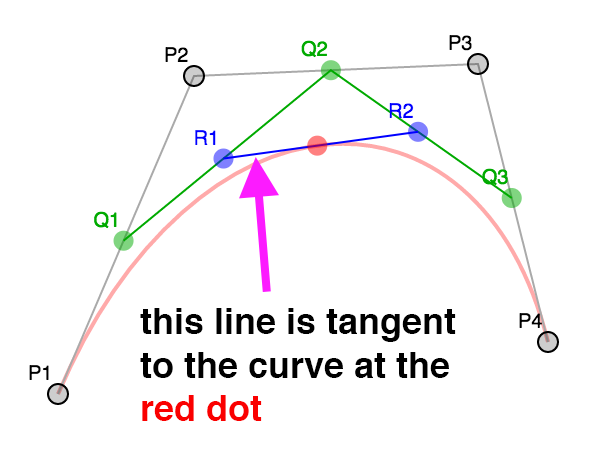
А нормаль - это перпендикуляр к касательной, поэтому, используя касательные, можно легко найти нормали.

Но давайте представим, что нам необходимо сделать подсвечник с подобным контуром:

Наряду со множеством гладких участков присутствуют и острые углы. Как понять, какие нормали использовать? Дело усугубляется тем, что для острых углов нужны дополнительные вершины. Вершины включают в себя как координату, так и нормаль, поэтому если нам нужна ещё одна нормаль, то нам нужна ещё одна вершина. Именно поэтому при создании куба нужно как минимум 24 вершины. Несмотря на то, что у куба всего 8 углов, каждая грань нуждается в отдельной нормали в каждом углу куба.

При создании куба задать правильные нормали очень просто, но для сложных фигур простого способа не найти.

Все программы для моделирования содержат разнообразные параметры создания нормалей. Обычно для каждой вершины находится усреднённая нормаль между всеми полигонами, в которые входит данная вершина. Но пользователь может задать максимальный угол. Если угол между полигонами с общей вершиной больше максимального, создаётся новая вершина.

Реализуем данный алгоритм.

function generateNormals(arrays, maxAngle) {
  const positions = arrays.position;
  const texcoords = arrays.texcoord;

  // сначала вычисляем нормаль для каждой грани
  let getNextIndex = makeIndiceIterator(arrays);
  const numFaceVerts = getNextIndex.numElements;
  const numVerts = arrays.position.length;
  const numFaces = numFaceVerts / 3;
  const faceNormals = [];

  // Вычисляем нормаль для каждой грани.
  // При этом создаём новую вершину для каждой грани
  for (let i = 0; i < numFaces; ++i) {
    const n1 = getNextIndex() * 3;
    const n2 = getNextIndex() * 3;
    const n3 = getNextIndex() * 3;

    const v1 = positions.slice(n1, n1 + 3);
    const v2 = positions.slice(n2, n2 + 3);
    const v3 = positions.slice(n3, n3 + 3);

    faceNormals.push(m4.normalize(m4.cross(m4.subtractVectors(v1, v2), m4.subtractVectors(v3, v2))));
  }

  let tempVerts = {};
  let tempVertNdx = 0;

  // предполагается, что координаты вершин точно совпадают между собой

  function getVertIndex(x, y, z) {

    const vertId = x + "," + y + "," + z;
    const ndx = tempVerts[vertId];
    if (ndx !== undefined) {
      return ndx;
    }
    const newNdx = tempVertNdx++;
    tempVerts[vertId] = newNdx;
    return newNdx;
  }

  // Находим вершины, принадлежащие нескольким граням.
  // При этом нельзя обращать внимание только на грани (треугольники)
  // так как, например, если у нас есть обыкновенный цилиндр,
  //
  //
  //      3-4
  //     /   \
  //    2     5   Если посмотреть на цилиндр, который начинается
  //    |     |   в точке S и заканчивается в E, точки E и S не
  //    1     6   являются одной и той же точкой с точки зрения
  //     \   /    входных данных, так как у них разные UV-координаты.
  //      S/E
  //
  // вершины в начале и в конце не будут принадлежать одной точке
  // так как у них разные UV-координаты, но если мы будем так
  // считать, мы получим неверные нормали.

  const vertIndices = [];
  for (let i = 0; i < numVerts; ++i) {
    const offset = i * 3;
    const vert = positions.slice(offset, offset + 3);
    vertIndices.push(getVertIndex(vert));
  }

  // проходим по каждой вершине и запоминаем, каким граням она принадлежит
  const vertFaces = [];
  getNextIndex.reset();
  for (let i = 0; i < numFaces; ++i) {
    for (let j = 0; j < 3; ++j) {
      const ndx = getNextIndex();
      const sharedNdx = vertIndices[ndx];
      let faces = vertFaces[sharedNdx];
      if (!faces) {
        faces = [];
        vertFaces[sharedNdx] = faces;
      }
      faces.push(i);
    }
  }

  // теперь проходим по каждой грани и вычисляем нормаль для каждой
  // вершины грани. Учитываются только те грани, которые в пределах
  // maxAngle. Результатом будут массивы newPositions, newTexcoords
  // и newNormals, за исключением одинаковых вершин.
  tempVerts = {};
  tempVertNdx = 0;
  const newPositions = [];
  const newTexcoords = [];
  const newNormals = [];

  function getNewVertIndex(x, y, z, nx, ny, nz, u, v) {
    const vertId =
        x + "," + y + "," + z + "," +
        nx + "," + ny + "," + nz + "," +
        u + "," + v;

    const ndx = tempVerts[vertId];
    if (ndx !== undefined) {
      return ndx;
    }
    const newNdx = tempVertNdx++;
    tempVerts[vertId] = newNdx;
    newPositions.push(x, y, z);
    newNormals.push(nx, ny, nz);
    newTexcoords.push(u, v);
    return newNdx;
  }

  const newVertIndices = [];
  getNextIndex.reset();
  const maxAngleCos = Math.cos(maxAngle);
  // для каждой грани
  for (let i = 0; i < numFaces; ++i) {
    // получаем нормаль текущей грани
    const thisFaceNormal = faceNormals[i];
    // для каждой вершины грани
    for (let j = 0; j < 3; ++j) {
      const ndx = getNextIndex();
      const sharedNdx = vertIndices[ndx];
      const faces = vertFaces[sharedNdx];
      const norm = [0, 0, 0];
      faces.forEach(faceNdx => {
        // грань направлена в ту же сторону?
        const otherFaceNormal = faceNormals[faceNdx];
        const dot = m4.dot(thisFaceNormal, otherFaceNormal);
        if (dot > maxAngleCos) {
          m4.addVectors(norm, otherFaceNormal, norm);
        }
      });
      m4.normalize(norm, norm);
      const poffset = ndx * 3;
      const toffset = ndx * 2;
      newVertIndices.push(getNewVertIndex(
          positions[poffset + 0], positions[poffset + 1], positions[poffset + 2],
          norm[0], norm[1], norm[2],
          texcoords[toffset + 0], texcoords[toffset + 1]));
    }
  }

  return {
    position: newPositions,
    texcoord: newTexcoords,
    normal: newNormals,
    indices: newVertIndices,
  };

}

function makeIndexedIndicesFn(arrays) {
  const indices = arrays.indices;
  let ndx = 0;
  const fn = function() {
    return indices[ndx++];
  };
  fn.reset = function() {
    ndx = 0;
  };
  fn.numElements = indices.length;
  return fn;
}

function makeUnindexedIndicesFn(arrays) {
  let ndx = 0;
  const fn = function() {
    return ndx++;
  };
  fn.reset = function() {
    ndx = 0;
  }
  fn.numElements = arrays.positions.length / 3;
  return fn;
}

function makeIndiceIterator(arrays) {
  return arrays.indices
      ? makeIndexedIndicesFn(arrays)
      : makeUnindexedIndicesFn(arrays);
}

В этом коде мы сначала создаём нормали для каждой грани (каждого треугольника) из исходных точек. Затем мы генерируем набор индексов вершин для нахождения одинаковых точек. После выполнения поворота первая и последняя точка должны совпадать, однако, они имеют разные UV-координаты и, следовательно, не считаются одинаковыми точками - именно поэтому нам нужен набор, где мы находим подобные точки. Для вычисления нормалей нам нужно, чтобы первая и последняя точка рассматривались как одна и та же точка.

После этого для каждой вершины мы находим все грани, в которых она используется.

И, наконец, мы усредняем нормали всех граней для каждой вершины, за исключением тех, которые превышают порог maxAngle - для таких мы создаём новый набор вершин.

Результат будет следующим:

Обратите внимание, что мы получили острые углы в необходимых нам местах. Попробуйте увеличить значение maxAngle и вы увидите, как острые углы становятся плавными, как только соседние грани получают усреднённую нормаль вместо отдельных наборов. Также попробуйте изменить divisions до значения 5 или 6, а затем увеличьте значение maxAngle так, чтобы даже острые углы получили плавный переход освещения. При изменении режима mode в значение lit мы увидим, как будет выглядеть объект при включении освещения - именно освещение является причиной, по которой мы так много внимания уделили нормалям.

Итак, что же мы узнали?

Мы узнали, что для создания 3D-данных НУЖНО ИСПОЛЬЗОВАТЬ ПРОГРАММУ ДЛЯ 3D-МОДЕЛИРОВАНИЯ!!! 😝

Для создания чего-то действительно полезного вам, вероятней всего, понадобится какой-нибудь UV-редактор. Такой редактор также поможет в оформлении конечных точек. Вместо ограниченного набора настроек при моделировании вы будете использовать функции редактора для добавления конечных точек и более простого создания UV-координат для них. Кроме того, редакторы поддерживают вытягивание граней и вытягивание по определённой траектории, работа которых должна быть довольно очевидной на вышеприведённых примерах моделирования.

Ссылки

В заключении хотел сказать, что не написал бы эту статью без замечательной статьи о кривых Безье.

Что здесь делает нахождение остатка деления?

Если посмотреть на функцию lathePoints, вы заметите нахождение остатка от деления при нахождении угла.

for (let division = 0; division <= numDivisions; ++division) {
  const u = division / numDivisions;
*  const angle = lerp(startAngle, endAngle, u) % (Math.PI * 2);

Зачем она здесь нужна?

При повороте точек вокруг своей оси нам нужно, чтобы первая и последняя точка совпадали. Math.sin(0) и Math.sin(Math.PI * 2) должны быть одним и тем же значением, но операции с плавающей точкой не совершенны, и даже когда значения очень близки, они всё же не не являются на 100% одинаковыми.

Это незначительно отличие повлияет на вычисление нормалей. Нам нужно знать все грани, в которых используется данная вершина. Нахождение этих граней основывается на сравнении вершин. Если две вершины равны, то для нас это становится одной вершиной. К сожалению, из-за отличий в значениях Math.sin(0) и Math.sin(Math.PI * 2) вершины не будут равны и не сольются в одну вершину. А значит, при вычислении нормалей не все грани попадут в вычисление, что приведёт к неверным нормалям.

Вот наглядный пример, что произойдёт

На месте замыкания контура можно увидеть шов, что происходит из-за едва заметных отличий в значениях первой и последней вершины.

Первой моей мыслью было изменить алгоритм таким образом, чтобы проверять вершины на равенство с какой-то погрешностью. Если вершины равны в пределах допустимой погрешности, то это одна и та же вершина. Что-то вроде такого:

const epsilon = 0.0001;
const tempVerts = [];
function getVertIndex(position) {
  if (tempVerts.length) {
    // находим ближайшую из существующих вершин
    let closestNdx = 0;
    let closestDistSq = v2.distanceSq(position, tempVerts[0]);
    for (let i = 1; i < tempVerts.length; ++i) {
      let distSq = v2.distanceSq(position, tempVerts[i]);
      if (distSq < closestDistSq) {
        closestDistSq = distSq;
        closestNdx = i;
      }
    }
    // данная вершина достаточно близко?
    if (closestDistSq < epsilon) {
      // да, возвращаем индекс существующей вершины
      return closestNdx;
    }
  }
  // одинаковая вершина не найдена, создаём её и возвращаем её индекс
  tempVerts.push(position);
  return tempVerts.length - 1;
}

И это сработало! Шов исчез. Но, к сожалению, данный алгоритм выполнялся несколько секунд и интерфейсом стало невозможно пользоваться. Так как сложность алгоритма возвросла до O^2. Если переместить слайдеры на максимум, мы можем получить около 20000 вершин. Для сложности O^2 получится под 300 миллионов итераций.

Я обыскал интернет в поисках простого решения и не нашёл его. Я думал поместить все точки в октодерево для более быстрого поиска совпадающих точек, но для одной статьи получалось многовато материала.

Именно тогда я понял, что если проблема заключается только в конечных точках, мне может помочь остаток от деления. Изначально код выглядел следующим образом:

  const angle = lerp(startAngle, endAngle, u);

Затем я его переписал на окончательный вариант

  const angle = lerp(startAngle, endAngle, u) % (Math.PI * 2);

Из-за применения операции остатка от деления для `angle`, значение `endAngle` равного `Math.PI * 2` становится нулём, а это то же значение, что и начальный угол. Шов ушёл и проблема была решена!

И даже при установке `distance` в значение 0.001 и `divisions` в значение 60, на моём компьютере пересчёт фигуры занимает около секунды. И хотя должны быть способы оптимизации моего алгоритма, я думаю, что создание сложных фигур - это медленная операция в целом. Это лишь один пример, почему 3D-игры могут выполняться на частоте 60fps, а 3D-редакторы могут работать на очень медленной частоте кадров.

const mat = m4.yRotation(angle);
...
points.forEach((p, ndx) => {
  const tp = m4.transformPoint(mat, [...p, 0]);
  ...

const s = Math.sin(angle);
const c = Math.cos(angle);
...
points.forEach((p, ndx) => {
  const x = p[0];
  const y = p[1];
  const z = p[2];
  const tp = [
    x * c - z * s,
    y,
    x * s + z * c,
  ];
  ...

   const mat = m4.axisRotation(userSuppliedAxis, angle);