Эта статья из серии, которая начинается с Основ WebGL, является продолжением предыдущей статьи о переносе геометрии.

Должен признать, что не имею понятия, как мне всё это объяснить и донести смысл, но разве такая мелочь сможет меня остановить?..

Для начала я хочу познакомить вас с так называемой "единичной окружностью". Если вы помните математику средней школы (да-да, и не смейте здесь засыпать!), окружность имеет радиус. Радиус окружности - это расстояние от центра окружности до её границы. Единичная окружность - это окружность с радиусом, равным единице.

Вот та самая единичная окружность.

Если вы потянете за синий кружок вокруг окружности, значения X и Y будут меняться. Они представляют положение точки на окружности. На самом верху Y равен 1, а X равен 0. Справа X равен 1, а Y равен 0.

Из того же курса школьной математики вы, вероятно, помните, что если значение умножить на единицу, оно не изменится. То есть 123 * 1 = 123. Довольно просто, правда? В каком-то смысле единичная окружность - тоже своего рода единица. Единица для вращения. То есть вы можете умножить что-либо на единичную окружность, и это будет похоже на умножение на единицу, только ещё произойдёт магия и объект повернётся.

Мы возьмём значения X и Y из любой точки единичной окружности, и умножим на них нашу геометрию из предыдущего примера.

В шейдере произойдут следующие изменения:

<script id="vertex-shader-2d" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
+uniform vec2 u_rotation;

void main() {
+  // Поворот вершины
+  vec2 rotatedPosition = vec2(
+     a_position.x * u_rotation.y + a_position.y * u_rotation.x,
+     a_position.y * u_rotation.y - a_position.x * u_rotation.x);

  // Затем перенос
*  vec2 position = rotatedPosition + u_translation;

Изменим JavaScript, чтобы можно было передать эти 2 значения.

  ...

+  var rotationLocation = gl.getUniformLocation(program, "u_rotation");

  ...

+  var rotation = [0, 1];

  ...

  // Отрисовка сцены
  function drawScene() {

    ...

    // Задаём перенос
    gl.uniform2fv(translationLocation, translation);

+    // Задаём вращение
+    gl.uniform2fv(rotationLocation, rotation);

    // Отрисовываем геометрию
    var primitiveType = gl.TRIANGLES;
    var offset = 0;
    var count = 18;  // буква 'F' из 6 треугольников, 3 точки на треугольник
    gl.drawArrays(primitiveType, offset, count);
  }

И получаем результат. Потяните за синий кружок на окружности для поворота или за слайдеры для переноса.

Как это работает? Взглянем на математику.

rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;

Скажем, у нас есть прямоугольник, который нужно перевернуть. Изначально его верхний правый угол находится в координатах 3.0, 9.0. Теперь возьмём точку на единичной окружности, смещённой на 30 градусам от 12 часов по направлению часовой стрелки.

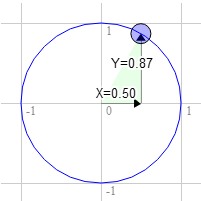
Положение на окружности в этом месте будет иметь значения 0.50 и 0.87.

   3.0 * 0.87 + 9.0 * 0.50 = 7.1
   9.0 * 0.87 - 3.0 * 0.50 = 6.3

Именно здесь нам и нужно быть.

То же самое для 60 градусов по часовой стрелке.

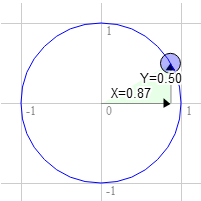
Положение на окружности в этом месте будет иметь значения 0.87 и 0.50

   3.0 * 0.50 + 9.0 * 0.87 = 9.3
   9.0 * 0.50 - 3.0 * 0.87 = 1.9

Вы можете заметить, что с поворотом по часовой стрелке значение X увеличивается, а значение Y уменьшается. Если мы перейдём за 90 градусов, X начнёт уменьшаться, а Y - увеличиваться. Это поведение и даёт нам поворот.

Точки на единичной окружности также известны под названиями синус и косинус. Поэтому для любого заданного угла мы можем получить значения синуса и косинуса следующим образом:

function printSineAndCosineForAnAngle(angleInDegrees) {
  var angleInRadians = angleInDegrees * Math.PI / 180;
  var s = Math.sin(angleInRadians);
  var c = Math.cos(angleInRadians);
  console.log("s = " + s + " c = " + c);
}

Если вы скопируете код и вставите его в консоль JavaScript, а затем введёте printSineAndCosignForAngle(30), то вы увидите s = 0.49 c = 0.87 (я округлил значения).

Если сложить всё вместе, мы можем поворачивать геометрию на любой заданный угол. Просто установите вращению значения синуса и косинуса угла, на который требуется выполнить поворот.

  ...
  var angleInRadians = angleInDegrees * Math.PI / 180;
  rotation[0] = Math.sin(angleInRadians);
  rotation[1] = Math.cos(angleInRadians);

Вот версия, где задаётся угол поворота. Используйте слайдеры для переноса или поворота.

Надеюсь, я донёс смысл. Такой способ задания поворота не является общепринятым, поэтому продолжайте чтение, мы дойдём до пункта назначения через две статьи. Следующая будет проще - масштабирование.