이 포스트는 WebGL 관련 시리즈에서 이어집니다. 첫 번째는 기초로 시작했고, 이전에는 3D 기초에 관한 것이었습니다. 아직 읽지 않으셨다면 해당 글들을 먼저 읽어주세요.

지난 포스트에서 어떻게 3D를 하는지 살펴봤지만 해당 3D는 어떤 원근감도 가지지 않았습니다. "직교 투영"이라 불리는 방법을 사용했는데 이건 사람들이 "3D"를 말할 때 일반적으로 원하는 게 아닙니다.

대신에 원근법을 추가해야 합니다. 원근법이 뭘까요? 기본적으로 더 멀리 있는 것들이 더 작게 보이는 방법입니다.

예시를 보면 더 멀리 있는 것들은 더 작게 그려지는 것을 볼 수 있습니다. 현재 샘플에서 더 멀리 있는 것들이 더 작게 보이도록 만드는 쉬운 방법은 클립 공간의 X와 Y를 Z로 나누는 겁니다.

(10, 15)에서 (20,15)까지 길이가 10인 선이 있다고 생각해보세요. 현재 샘플에서 이 선은 10픽셀의 길이로 그려질 겁니다. 하지만 Z로 나눈다면,

10 / 1 = 10
20 / 1 = 20
abs(10-20) = 10

Z가 1인 경우 길이는 10픽셀이 됩니다.

10 / 2 = 5
20 / 2 = 10
abs(5 - 10) = 5

Z가 2인 경우에는 5픽셀이 되죠.

10 / 3 = 3.333
20 / 3 = 6.666
abs(3.333 - 6.666) = 3.333

Z가 증가할수록, 멀어질수록, 더 작게 그려지는 걸 볼 수 있습니다. 클립 공간에서 나누면 Z가 더 작은 숫자(-1 ~ +1)이기 때문에 더 나은 결과를 얻을 수 있는데요. 나누기 전에 Z를 fudgeFactor와 곱하면 주어진 거리에 따라 얼마나 작게 할지 조정할 수 있습니다.

한 번 해봅시다. 먼저 "fudgeFactor"를 곱한 뒤 Z로 나누도록 정점 셰이더를 수정합니다.

<script id="vertex-shader-3d" type="x-shader/x-vertex">
...
+uniform float u_fudgeFactor;
...
void main() {
  // 위치에 행렬 곱하기
  vec4 position = u_matrix * a_position;

+  // 나누려는 z 조정
+  float zToDivideBy = 1.0 + position.z * u_fudgeFactor;

*  // x와 y를 z로 나누기
*  gl_Position = vec4(position.xy / zToDivideBy, position.zw);
}
</script>

참고로 Z가 -1에서 +1인 클립 공간에 있기 때문에, 0에서 +2 * fudgeFactor인 zToDivideBy를 얻기 위해 1을 더했습니다.

또한 fudgeFactor를 설정할 수 있도록 코드를 업데이트해야 합니다.

  ...
  var fudgeLocation = gl.getUniformLocation(program, "u_fudgeFactor");

  ...
  var fudgeFactor = 1;
  ...
  function drawScene() {
    ...
    // fudgeFactor 설정
    gl.uniform1f(fudgeLocation, fudgeFactor);

    // 지오메트리 그리기
    var primitiveType = gl.TRIANGLES;
    var offset = 0;
    var count = 16 * 6;
    gl.drawArrays(primitiveType, offset, count);

그리고 여기 결과입니다.

알아보기 힘들다면 Z로 나누는 코드를 추가하기 전 어떤 모습이었는지 보기 위해 "fudgeFactor" 슬라이더를 1.0에서 0.0으로 드래그해보세요.

WebGL은 정점 셰이더의 gl_Position에 할당한 x,y,z,w 값을 가져와 자동으로 w로 나눕니다.

이는 셰이더를 변경하여 직접 나누는 대신, gl_Position.w에 zToDivideBy를 넣어서 쉽게 증명할 수 있습니다.

<script id="vertex-shader-2d" type="x-shader/x-vertex">
...
uniform float u_fudgeFactor;
...
void main() {
  // 위치에 행렬 곱하기
  vec4 position = u_matrix * a_position;

  // 나누려는 z 조정
  float zToDivideBy = 1.0 + position.z * u_fudgeFactor;

  // x, y, z를 zToDivideBy로 나누기
*  gl_Position = vec4(position.xyz, zToDivideBy);

  // 프래그먼트 셰이더로 색상 전달
  v_color = a_color;
}
</script>

그리고 얼마나 정확하게 일치하는지 봅시다.

WebGL이 알아서 W로 나눈다는 사실이 유용한 이유는 뭘까요? 그 이유는 이제 더 많은 행렬을 사용하여 z를 w에 복사하기 위해 또 다른 행렬을 사용할 수 있기 때문입니다.

이런 행렬이 z를 w에 복사할 겁니다.

1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 1,
0, 0, 0, 0,

각 열을 다음과 같이 볼 수 있으며,

x_out = x_in * 1 +
        y_in * 0 +
        z_in * 0 +
        w_in * 0 ;

y_out = x_in * 0 +
        y_in * 1 +
        z_in * 0 +
        w_in * 0 ;

z_out = x_in * 0 +
        y_in * 0 +
        z_in * 1 +
        w_in * 0 ;

w_out = x_in * 0 +
        y_in * 0 +
        z_in * 1 +
        w_in * 0 ;

이를 단순화하면,

x_out = x_in;
y_out = y_in;
z_out = z_in;
w_out = z_in;

우리는 w_in이 항상 1.0이라는 걸 알기 때문에 이전에 가졌던 +1을 이 행렬에 추가할 수 있습니다.

1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 1,
0, 0, 0, 1,

다음과 같이 W 계산이 바뀌고,

w_out = x_in * 0 +
        y_in * 0 +
        z_in * 1 +
        w_in * 1 ;

w_in = 1.0인 것을 알기 때문에 이렇게 변경할 수 있습니다.

w_out = z_in + 1;

마지막으로 행렬이 아래와 같으면 fudgeFactor를 다시 사용할 수 있는데,

1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, fudgeFactor,
0, 0, 0, 1,

이게 의미하는 것은 다음과 같습니다.

w_out = x_in * 0 +
        y_in * 0 +
        z_in * fudgeFactor +
        w_in * 1 ;

그리고 단순화하면 이렇게 됩니다.

w_out = z_in * fudgeFactor + 1;

이제 행렬만 사용하도록 다시 프로그램을 수정해봅시다.

먼저 정점 셰이더를 되돌립니다.

<script id="vertex-shader-2d" type="x-shader/x-vertex">
uniform mat4 u_matrix;

void main() {
  // 위치에 행렬 곱하기
  gl_Position = u_matrix * a_position;
  ...
}
</script>

다음으로 Z → W 행렬을 만드는 함수를 만들어 봅시다.

function makeZToWMatrix(fudgeFactor) {
  return [
    1, 0, 0, 0,
    0, 1, 0, 0,
    0, 0, 1, fudgeFactor,
    0, 0, 0, 1,
  ];
}

그리고 그걸 사용하도록 코드를 변경할 겁니다.

    ...
    // 행렬 계산
*    var matrix = makeZToWMatrix(fudgeFactor);
*    matrix = m4.multiply(matrix, m4.projection(gl.canvas.clientWidth, gl.canvas.clientHeight, 400));
    matrix = m4.translate(matrix, translation[0], translation[1], translation[2]);
    matrix = m4.xRotate(matrix, rotation[0]);
    matrix = m4.yRotate(matrix, rotation[1]);
    matrix = m4.zRotate(matrix, rotation[2]);
    matrix = m4.scale(matrix, scale[0], scale[1], scale[2]);

    ...

그리고 다시 말하지만 정확하게 일치합니다.

기본적으로 모든 내용들은 Z로 나누는 게 원근감을 준다는 것과 WebGL이 편리하게 Z로 나누는 작업을 해준다는 걸 보여주기 위한 겁니다.

하지만 여전히 몇 가지 문제가 있습니다. 예를 들어 Z를 -100 정도로 설정하면 아래와 같은 애니메이션을 보게 됩니다.

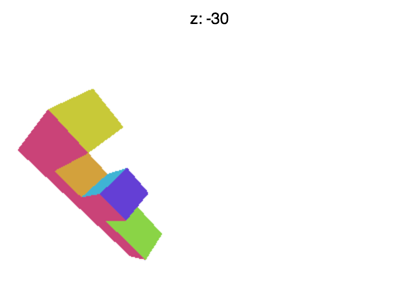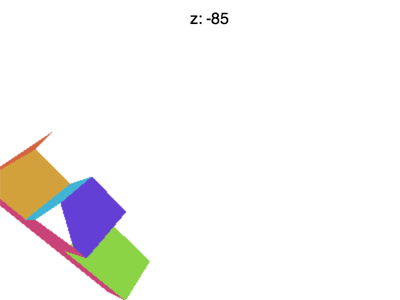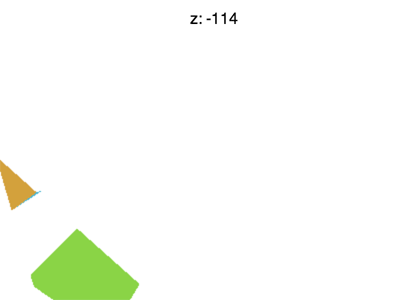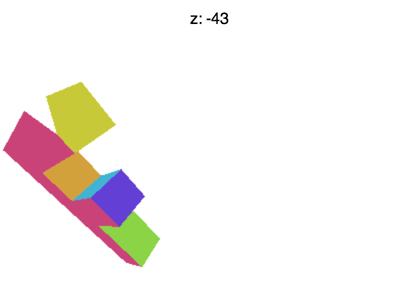
어떻게 된거죠? F가 일찍 사라지는 이유는 뭘까요? WebGL은 X와 Y 혹은 +1에서 -1까지 클리핑하는 것처럼 Z도 클리핑하는데요. 여기서 우리가 보고 있는 건 Z < -1 입니다.

이를 해결하기 위해 수학에 대한 자세한 설명을 할 수도 있지만 2D 투영을 했던 것과 같은 방법으로 도출할 수도 있습니다. Z를 가져와 어느정도 더하고 크기 조정하여 원하는 범위를 -1에서 +1사이로 다시 매핑할 수 있습니다.

멋진 점은 이 모든 단계를 하나의 행렬로 수행할 수 있다는 겁니다. 더 좋은 점은 fudgeFactor 대신에 fieldOfView를 결정하고 이를 위한 올바른 값을 계산한다는 겁니다.

다음은 행렬을 만드는 함수입니다.

var m4 = {
  perspective: function(fieldOfViewInRadians, aspect, near, far) {
    var f = Math.tan(Math.PI * 0.5 - 0.5 * fieldOfViewInRadians);
    var rangeInv = 1.0 / (near - far);

    return [
      f / aspect, 0, 0, 0,
      0, f, 0, 0,
      0, 0, (near + far) * rangeInv, -1,
      0, 0, near * far * rangeInv * 2, 0
    ];
  },

  ...

이 행렬이 모든 변환을 수행할 겁니다. 단위가 클립 공간 안에 있도록 조정되며, 각도별로 시야각을 선택할 수 있고, Z-클리핑 공간을 선택할 수 있게 되는데요. 원점(0, 0, 0)에 눈이나 카메라가 있다고 가정하고, zNear와 fieldOfView가 주어지면, zNear의 항목이 Z = -1이 되는데 필요한 값을 계산하며, fieldOfView의 절반인 zNear의 위와 아래는 각각 Y = -1과 Y = 1이 됩니다. 그리고 전달된 aspect를 곱하여 X에 사용할 값을 계산하는데요. 일반적으로 디스플레이 영역의 width / height로 설정합니다. 마지막으로 zFar의 항목이 Z = 1이 되도록 하기 위해 Z에서 얼마나 크기를 조정할지 알아냅니다.

다음은 실행중인 행렬의 다이어그램입니다.

내부에서 큐브가 회전하고 있는 4면 원뿔 모양을 "절두체"라고 합니다. 행렬은 절두체 안에 있는 공간을 가져와서 클립 공간으로 변환하는데요. zNear은 물체의 앞쪽이 잘리는 곳을 정의하고, zFar은 물체의 뒤쪽이 잘리는 곳을 정의합니다. zNear을 23으로 설정하면 회전하는 큐브의 앞면이 잘리는 걸 볼 수 있죠. zFar을 24로 설정하면 큐브의 뒷면이 잘리는 걸 볼 수 있습니다.

이제 남은 문제는 단 하나입니다. 이 행렬은 0,0,0에 뷰어가 있다고 가정하고, -Z 방향으로 바라보며 +Y가 위를 향하고 있다고 가정하는데요. 지금까지의 행렬은 다른 방식으로 작업을 수행했습니다.

이걸 보이게 하려면 절두체 안으로 옮겨야 합니다. F를 움직이면 되는데요. 기존에는 (45, 150, 0)에 그리고 있었습니다. 이걸 (-150, 0, -360)로 옮기고 오른쪽이 위로 보이도록 회전을 설정합시다.

이제 이걸 사용하려면 m4.projection에 대한 기존 호출을 m4.perspective에 대한 호출로 바꾸면 됩니다.

var aspect = gl.canvas.clientWidth / gl.canvas.clientHeight;
var zNear = 1;
var zFar = 2000;
var matrix = m4.perspective(fieldOfViewRadians, aspect, zNear, zFar);
matrix = m4.translate(matrix, translation[0], translation[1], translation[2]);
matrix = m4.xRotate(matrix, rotation[0]);
matrix = m4.yRotate(matrix, rotation[1]);
matrix = m4.zRotate(matrix, rotation[2]);
matrix = m4.scale(matrix, scale[0], scale[1], scale[2]);

그리고 여기 결과입니다.

다시 행렬 곱셉으로 돌아가서 시야각을 확보하고 Z 공간을 선택할 수 있습니다. 아직 끝나지 않았지만 글이 너무 길어지고 있군요. 다음은 카메라입니다.

F를 Z(-360)로 옮긴 이유가 뭔가요?

다른 샘플에서는 F가 (45, 150, 0)에 있지만 마지막 샘플에서는 (-150, 0, -360)으로 옮겨졌습니다. 왜 그렇게 멀리 옮겨야 했을까요?

그 이유는 마지막 샘플까지 m4.projection 함수가 픽셀에서 클립 공간으로 투영했기 때문입니다. 이는 우리가 표시하고 있던 영역이 400x300픽셀로 표현되었다는 의미인데요. 3D에서 '픽셀'을 사용하는 것은 실제로 의미가 없습니다.

다시말해 0,0,0에서 F를 그리려고 했지만 회전하지 않는다면 F는 원점의 왼쪽 상단 모서리의 앞쪽에 있게 됩니다. 투영은 -Z를 향하지만 F는 +Z로 만들어졌죠. 투영은 +Y가 위를 향하지만 F는 +Z가 아래를 향합니다.

새로운 투영은 파란 절두체 안에 있는 것만 볼 수 있습니다. -zNear = 1 그리고 60도의 시야각일 때 Z = -1에서 절두체의 높이는 1.154이고 너비는 1.154 * aspect 입니다. Z = -2000 (-zFar)에서 높이는 2309입니다. F의 크기가 150이고, -zNear에 무언가가 있을 때 뷰는 1.154만 볼 수 있기 때문에, 모든 걸 보려면 원점에서 꽤 멀리 이동해야 합니다.

Z에서 -360만큼 움직이면 절두체의 내부로 이동합니다. 또한 오른쪽이 위쪽을 향하도록 회전시켰습니다.

스케일 없음