이 포스트는 WebGL 관련 시리즈에서 이어집니다. 첫 번째는 기초로 시작했고, 이전에는 지오메트리 평행 이동에 관한 것이었습니다.

솔직히 이걸 어떻게 설명해야 할지 모르겠지만 뭐 어때요. 시도는 해봅시다.

먼저 "단위원"에 대해 소개하려고 합니다. 중학교 수학을 기억해보면(저처럼 졸지 마세요!) 원은 반지름을 가지는데요. 원의 반지름은 원의 중심에서 가장자리까지의 거리입니다. 단위원은 반지름이 1.0인 원입니다.

이게 바로 단위원입니다.

참고로 파란색 핸들을 원 주위로 드래그하면 X와 Y의 위치가 변경됩니다. 이것들은 원 위에 있는 점의 위치를 나타내는데요. 위쪽일 때 Y는 1이고 X는 0입니다. 오른쪽일 때 X는 1이고 Y는 0입니다.

3학년 기초 수학을 기억해보면 뭔가에 1을 곱해도 값은 그대로 유지됩니다. 그래서 123 * 1 = 123 입니다. 아주 기본적이죠? 단위원, 반지름이 1.0인 원도 1과 동일한데요. 회전하는 1입니다. 그래서 무언가를 단위원에 곱하면 이는 1을 곱하는 것과 같습니다.

단위원의 어느 지점에서 X와 Y값을 가져와서 이전 샘플의 지오메트리에 곱해봅시다.

다음은 셰이더 변경 사항입니다.

<script id="vertex-shader-2d" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
+uniform vec2 u_rotation;

void main() {
+  // 위치 회전
+  vec2 rotatedPosition = vec2(
+     a_position.x * u_rotation.y + a_position.y * u_rotation.x,
+     a_position.y * u_rotation.y - a_position.x * u_rotation.x);

  // 평행 이동 추가
*  vec2 position = rotatedPosition + u_translation;

그리고 자바스크립트를 업데이트해서 두 값을 전달할 수 있습니다.

  ...

+  var rotationLocation = gl.getUniformLocation(program, "u_rotation");

  ...

+  var rotation = [0, 1];

  ...

  // 장면 그리기
  function drawScene() {

    ...

    // 평행 이동 설정
    gl.uniform2fv(translationLocation, translation);

+    // 회전 설정
+    gl.uniform2fv(rotationLocation, rotation);

    // 지오메트리 그리기
    var primitiveType = gl.TRIANGLES;
    var offset = 0;
    var count = 18;  // 'F'의 삼각형 6개, 삼각형마다 점 3개
    gl.drawArrays(primitiveType, offset, count);
  }

그리고 여기 결과물입니다. 원 위에 있는 핸들을 드래그해서 회전시키거나 슬라이더를 드래그해서 이동시켜보세요.

왜 작동하는 걸까요? 수식을 봅시다.

rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;

사각형이 하나 있고 그걸 회전시키고 싶다고 해봅시다. 회전을 시작하기 전 오른쪽 상단 모서리는 3.0, 9.0 입니다. 단위원의 12시에서 시계 방향 30도 지점을 선택해봅시다.

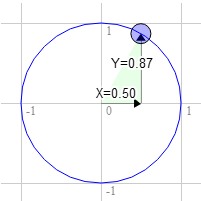
원의 위치는 0.50와 0.87에 있는데,

   3.0 * 0.87 + 9.0 * 0.50 = 7.1
   9.0 * 0.87 - 3.0 * 0.50 = 6.3

그게 우리가 필요로 하는 곳이며,

시계방향 60도 또한 동일하게,

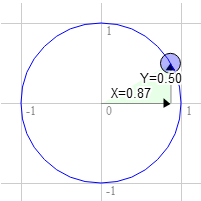
원의 위치는 0.87과 0.50에 있고,

   3.0 * 0.50 + 9.0 * 0.87 = 9.3
   9.0 * 0.50 - 3.0 * 0.87 = 1.9

점을 오른쪽 시계 방향으로 돌리면 X값은 커지고 Y는 작아지는 걸 볼 수 있습니다. 계속 돌려서 90도를 넘으면 X는 다시 작아지고 Y는 커지는데요. 이 패턴은 회전이 가능하게 해줍니다.

단위원의 점은 또 다른 이름이 있습니다. 이를 사인과 코사인이라고 합니다. 따라서 주어진 각도의 사인과 코사인을 이렇게 찾을 수 있습니다.

function printSineAndCosineForAnAngle(angleInDegrees) {
  var angleInRadians = angleInDegrees * Math.PI / 180;
  var s = Math.sin(angleInRadians);
  var c = Math.cos(angleInRadians);
  console.log("s = " + s + " c = " + c);
}

자바스크립트 콘솔에 코드를 복사하고 printSineAndCosignForAngle(30)이라고 치면 s = 0.49 c = 0.87이 출력됩니다. (참고: 숫자는 반올림했습니다.)

전부 합치면 지오메트리를 원하는 각도로 회전할 수 있습니다. 그저 돌리고 싶은 각도의 사인과 코사인으로 rotation을 설정하면 됩니다.

  ...
  var angleInRadians = angleInDegrees * Math.PI / 180;
  rotation[0] = Math.sin(angleInRadians);
  rotation[1] = Math.cos(angleInRadians);

다음은 슬라이더로 각도를 설정할 수 있는 버전입니다. 슬라이더를 드래그해서 평행 이동하거나 회전시켜보세요.

회전을 수행하는 일반적인 방법은 아니지만 2개의 글에서 더 다룰테니 계속 읽어주세요. 다음은 더 간단한 스케일입니다.