WebGL 3D - 스포트라이트
이 글은 WebGL 3D 점 조명에서 이어집니다. 아직 읽지 않았다면 거기부터 시작하는 게 좋습니다.
지난 글에서 우리는 조명에서 물체 표면의 모든 지점까지의 방향을 계산하는 점 조명에 대해 알아봤습니다. 그런 다음 방향성 조명에서 했던 것과 동일하게 표면 법선(표면이 향하는 방향)과 조명 방향의 스칼라곱을 구했는데요. 두 방향이 일치해서 완전히 밝아져야 하는 경우 1이 됩니다. 두 방향이 수직이면 0이고 반대면 -1이 되죠. 조명이 비추는 표면의 색상에 곱하기 위해 해당 값을 사용했습니다.
스포트라이트는 아주 약간 달라집니다. 사실 지금까지 했던 것을 생각해보면 여러분만의 창의적인 해결책을 도출할 수 있을 겁니다.
점 조명은 한 지점에서 모든 방향으로 진행하는 빛을 가진다고 상상할 수 있습니다. 스포트라이트를 만들기 위해서는 해당 지점에서 스포트라이트의 방향을 선택하면 됩니다. 그러면 빛이 진행하는 모든 방향에 대해 해당 방향과 우리가 선택한 스포트라이트 방향의 스칼라곱을 구할 수 있습니다. 임의의 임계값을 정하고 해당 임계값 내에 있다면 조명을 비춥니다. 해당 임계값 내에 없다면 조명을 비추지 않게 됩니다.
위 다이어그램에서 광선이 모든 방향으로 진행되고 방향에 대한 스칼라곱이 표시되는 것을 볼 수 있습니다. 또한 스포트라이트의 방향인 direction을 가집니다. 그리고 limit(각도)를 설정하는데요. 임계값으로 dot limit를 계산하고 임계값의 코사인을 구합니다. 각 광선의 방향과 우리가 선택한 스포트라이트 방향의 스칼라곱이 dot limit를 초과하면 조명이 작동합니다.
조금 다른 말로 설명하기 위해 임계값이 20도라고 가정해봅시다. 이걸 라디안으로 변환하고 코사인을 적용해서 -1에서 1사이의 값으로 만들 수 있는데요. 이를 dot space라고 부릅시다. 다음은 임계값 값에 대한 표입니다.
단위별 임계값
각도 | 라디안 | dot space
--------+---------+----------
0 | 0.0 | 1.0
22 | .38 | .93
45 | .79 | .71
67 | 1.17 | .39
90 | 1.57 | 0.0
180 | 3.14 | -1.0
그러면 조명 작동 여부를 바로 확인할 수 있습니다.
dotFromDirection = dot(surfaceToLight, -lightDirection)
if (dotFromDirection >= limitInDotSpace) {
// 조명 작동
}
이렇게 작동하도록 만들어봅시다.
먼저 지난 글의 프래그먼트 셰이더를 수정합니다.
precision mediump float;
// 정점 셰이더에서 전달됩니다.
varying vec3 v_normal;
varying vec3 v_surfaceToLight;
varying vec3 v_surfaceToView;
uniform vec4 u_color;
uniform float u_shininess;
+uniform vec3 u_lightDirection;
+uniform float u_limit; // dot space
void main() {
// v_normal은 varying이기 때문에 보간되므로 단위 벡터가 아닙니다.
// 정규화하면 다시 단위 벡터가 됩니다.
vec3 normal = normalize(v_normal);
vec3 surfaceToLightDirection = normalize(v_surfaceToLight);
vec3 surfaceToViewDirection = normalize(v_surfaceToView);
vec3 halfVector = normalize(surfaceToLightDirection + surfaceToViewDirection);
- float light = dot(normal, surfaceToLightDirection);
+ float light = 0.0;
float specular = 0.0;
+ float dotFromDirection = dot(surfaceToLightDirection, -u_lightDirection);
+ if (dotFromDirection >= u_limit) {
* light = dot(normal, surfaceToLightDirection);
* if (light > 0.0) {
* specular = pow(dot(normal, halfVector), u_shininess);
* }
+ }
gl_FragColor = u_color;
// 색상 부분(알파 제외)에만 light 곱하기
gl_FragColor.rgb *= light;
// 반사율 더하기
gl_FragColor.rgb += specular;
}
추가한 유니폼의 위치를 찾아야 합니다.
var lightDirection = [?, ?, ?];
var limit = degToRad(20);
...
var lightDirectionLocation = gl.getUniformLocation(program, "u_lightDirection");
var limitLocation = gl.getUniformLocation(program, "u_limit");
이제 그걸 설정해야 합니다.
gl.uniform3fv(lightDirectionLocation, lightDirection);
gl.uniform1f(limitLocation, Math.cos(limit));
그리고 여기 결과입니다.
몇 가지 주의할 사항: 위에서 u_lightDirection을 음수화하고 있습니다.
우리는 비교할 두 방향이 일치할 때 같은 방향을 가리키길 원하는데요.
즉 surfaceToLightDirection을 스포트라이트의 반대 방향과 비교해야 합니다.
여러 가지 다른 방법으로 이를 수행할 수 있습니다.
한 가지 방법으로 유니폼을 설정할 때 음수 방향을 전달할 수 있는데요.
제가 가장 선호하는 방식이지만 이 경우 유니폼을 u_reverseLightDirection이나 u_negativeLightDirection 대신 u_lightDirection이라 부르는 것이 덜 혼란스러울 것 같습니다.
제 개인적인 취향이지만 가능하면 셰이더에서 조건문 쓰고 싶지 않습니다. 그 이유는 사실 셰이더에는 조건문이 없기 때문입니다. 조건문을 추가하면 코드에 여기 저기에 0과 1로 곱하는 코드를 확장하여 실제로는 조건문이 없도록 만듭니다. 즉 조건문을 추가하면 조합의 확장으로 코드가 터질 수 있습니다. 지금도 그런지는 모르겠지만 몇 가지 기술도 보여드릴 겸 조건문을 제거해보겠습니다. 사용 여부는 스스로 결정하시면 됩니다.
step이라 불리는 GLSL 함수가 있습니다.
2개의 값을 받는데 두 번째 값이 첫 번째 값보다 크거나 같으면 1.0을 반환합니다.
그 외에는 0을 반환합니다.
자바스크립트에서는 이렇게 작성할 수 있습니다.
function step(a, b) {
if (b >= a) {
return 1;
} else {
return 0;
}
}
조건문을 제거하기 위해 step을 사용해봅시다.
float dotFromDirection = dot(surfaceToLightDirection, -u_lightDirection);
// 스포트라이트 안에 있다면 "inLight"는 1이 되고 아니라면 0이 될 겁니다.
float inLight = step(u_limit, dotFromDirection);
float light = inLight * dot(normal, surfaceToLightDirection);
float specular = inLight * pow(dot(normal, halfVector), u_shininess);
시각적으로 변한 것은 없지만 이런 결과가 나옵니다.
한 가지 다른 점으로 현재 스포트라이트는 굉장히 엄격합니다. 스포트라이트 안에 있거나 아니거나 둘 중 하나이며 바깥에 있는 것들은 그냥 검은색으로 변해버립니다.
이를 수정하기 위해 1개 대신 2개(내부/외부)의 임계값을 사용할 수 있는데요. 내부 임계값 안에 있다면 1.0을 사용합니다. 외부 임계값 바깥에 있다면 0.0을 사용합니다. 내부 임계값과 외부 임계값 사이에 있다면 1.0과 0.0 사이로 선형 보간합니다.
다음은 이를 수행할 수 있는 하나의 방법입니다.
-uniform float u_limit; // dot space
+uniform float u_innerLimit; // dot space
+uniform float u_outerLimit; // dot space
...
float dotFromDirection = dot(surfaceToLightDirection, -u_lightDirection);
- float inLight = step(u_limit, dotFromDirection);
+ float limitRange = u_innerLimit - u_outerLimit;
+ float inLight = clamp((dotFromDirection - u_outerLimit) / limitRange, 0.0, 1.0);
float light = inLight * dot(normal, surfaceToLightDirection);
float specular = inLight * pow(dot(normal, halfVector), u_shininess);
그리고 이렇게 작동합니다.
이제 좀 더 스포트라이트처럼 보이네요!
한 가지 주의해야 할 것은 u_innerLimit과 u_outerLimit이 같으면 limitRange는 0.0이 됩니다.
우리는 limitRange로 나누고 있는데 0으로 나누는 것은 잘못되거나 정의되지 않은 동작을 야기하는데요.
이를 위해 자바스크립트에서 u_innerLimit가 u_outerLimit와 같지 않다는 것을 확인해야 합니다.
(참고: 예제 코드는 이를 수행하지 않습니다)
GLSL에는 이를 어느정도 단순화하기 위해 사용할 수 있는 함수도 있는데요.
smoothstep이라 불리고, step처럼 0에서 1사이의 값을 반환하지만, 하한과 상한이 필요하며, 그 범위의 0과 1 사이로 선형 보간됩니다.
smoothstep(lowerBound, upperBound, value)
이렇게 해봅시다.
float dotFromDirection = dot(surfaceToLightDirection, -u_lightDirection);
- float limitRange = u_innerLimit - u_outerLimit;
- float inLight = clamp((dotFromDirection - u_outerLimit) / limitRange, 0.0, 1.0);
float inLight = smoothstep(u_outerLimit, u_innerLimit, dotFromDirection);
float light = inLight * dot(normal, surfaceToLightDirection);
float specular = inLight * pow(dot(normal, halfVector), u_shininess);
이 또한 작동합니다.
차이점은 smoothstep의 경우 선형 보간법 대신 에르미트 보간법을 사용한다는 겁니다.
즉 lowerBound와 upperBound의 사이에서 아래 오른쪽 이미지처럼 보간하는 반면 선형 보간법은 왼쪽 이미지와 같습니다.
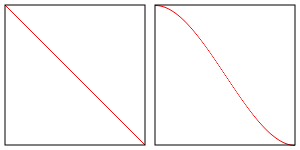
이 차이점을 중요하게 생각할지는 여러분이 선택하시면 됩니다.
한 가지 유의해야 할 다른 점은 smoothstep 함수는 lowerBound가 upperBound보다 크거나 같으면 정의되지 않은 결과가 나온다는 겁니다.
값이 같은 건 우리가 위에서 했던 것과 동일한 문제입니다.
lowerBound가 upperBound보다 큰 경우는 정의되지 않은 새로운 문제지만 절대 참이 되면 안 됩니다.