애매한 종류의 주제일 수 있지만 저는 흥미롭게 봐서 이 글을 작성하고 있습니다. 실제로 하라고 추천하는 것은 아닙니다. 그보다는 이 주제를 이용해 작업하는 게 WebGL용 3D 모델을 만드는 방법을 설명하는 데 도움이 될 것이라 생각합니다.

어떤 사람이 WebGL에서 볼링핀 모양을 만드는 방법을 물어봤습니다. 똑똑한 대답은 "Blender, Maya, 3D Studio Max, Cinema 4D와 같은 3D 모델링 패키지를 사용하세요" 입니다. 이를 사용하여 볼링핀을 모델링하고, 추출한 다음, 데이터를 읽습니다. OBJ 포맷은 비교적 간단합니다.

하지만 모델링 패키지를 만들고 싶다면 어떻게 해야 할까요?

몇 가지 아이디어가 있습니다. 하나는 원기둥을 만들고 특정 위치에 사인파를 적용하여 올바른 위치에 끼우는 겁니다. 해당 아이디어의 문제는 매끄러운 상판을 얻을 수 없다는 건데요. 표준 원기둥은 동일한 간격을 가진 일련의 고리로 생성되지만 굴곡이 많을수록 더 많은 고리가 필요합니다.

모델링 패키지에서는 2D 실루엣 혹은 2D 실루엣의 가장자리와 일치하는 곡선을 만들어 볼링핀을 만듭니다. 그런 다음 그걸 3D 모양으로 선반 처리하는데요. 선반이란 어떤 축을 중심으로 회전하여 점들을 생성한다는 의미입니다. 이렇게 하면 그릇, 유리잔, 야구 방망이, 병, 전구처럼 둥근 물체를 쉽게 만들 수 있습니다.

그래서 어떻게 해야 할까요? 먼저 곡선을 만드는 방법이 필요합니다. 그리고 해당 곡선의 점들을 계산해야 합니다. 그런 다음 행렬 수학을 사용하여 어떤 축을 중심으로 해당 점들을 회전시키고 이를 기준으로 삼각형을 만듭니다.

컴퓨터 그래픽에서 가장 흔한 곡선의 종류는 베지에 곡선인 것 같습니다. Adobe Illustrator나 Inkscape나 Affinity Designer 혹은 비슷한 프로그램에서 곡선을 편집해본 적이 있다면 그게 베지에 곡선입니다.

베지에 곡선이나 큐빅 베지에 곡선은 4개의 점으로 구성됩니다. 점 2개는 끝점이고 나머지 2개는 "제어점"입니다.

여기 4개의 점이 있습니다.

0이 시작이고 1이 끝일 때 0과 1사이의 숫자(이하 t)를 선택합니다. 그런 다음 두 점(P1 P2, P2 P3, P3 P4) 사이에 있는 점 t를 계산합니다.

즉 t = .25이면 P1에서 P2로 가는 경로의 25%, P2에서 P3로 가는 경로의 25%, P3에서 P4로 가는 경로의 25% 지점을 계산합니다.

슬라이더를 드래그하여 t를 조정할 수 있고 점 P1, P2, P3, P4를 이동할 수도 있습니다.

결과 지점에 대해서도 동일한 작업을 수행합니다. Q1 Q2과 Q2 Q3 사이에 있는 점 t를 계산합니다.

마지막으로 2개의 점에 대해서도 동일한 작업을 수행하고 R1 R2 사이의 점 t를 계산합니다.

빨간 점의 위치가 곡선을 만듭니다.

이게 큐빅 베지에 곡선입니다.

참고로 위 점들 사이의 보간과 4개를 3개로, 3개를 2개로, 마지막으로 2개를 1개의 점으로 만드는 과정은 정상적인 방법이 아닌데요. 이를 대신하기 위해 누군가가 모든 수식을 연결하여 이렇게 공식을 단순화했습니다.

invT = (1 - t)
P = P1 * invT^3 +
    P2 * 3 * t * invT^2 +
    P3 * 3 * invT * t^2 +
    P4 * t^3

여기서 P1, P2, P3, P4는 위 예제와 같은 점이고 P는 빨간 점입니다.

어도비 일러스트레이터처럼 2D 벡터 미술 프로그램에서 긴 곡선을 만들면 실제로 이렇게 다수의 작은 점 4개로 만들어집니다. 기본적으로 대부분의 앱은 공유된 시작/끝점을 중심으로 제어점을 고정하고 공유된 지점을 기준으로 항상 반대 방향에 있도록 합니다.

이 예제를 보면 P3나 P5를 움직일 때 코드가 다른 쪽을 움직일 겁니다.

P1,P2,P3,P4로 만들어진 곡선은 P4,P5,P6,P7로 만들어진 곡선과는 별개의 곡선입니다. P3와 P5가 P4 양쪽의 정반대에 있을 때 연속된 하나의 곡선처럼 보이는데요. 대부분의 앱은 가파른 곡선을 만들 수 있도록 고정을 푸는 옵션을 함께 제공합니다. 고정 체크 박스를 해제한 다음 P3나 P5를 드래그해보면 별개의 곡선이라는 것을 훨씬 더 명확하게 알 수 있습니다.

다음으로 곡선의 점들을 생성하는 방법이 필요합니다. 위 공식을 사용하여 다음과 같이 주어진 값 t에 대한 점을 생성할 수 있습니다.

function getPointOnBezierCurve(points, offset, t) {
  const invT = (1 - t);
  return v2.add(v2.mult(points[offset + 0], invT * invT * invT),
                v2.mult(points[offset + 1], 3 * t * invT * invT),
                v2.mult(points[offset + 2], 3 * invT * t * t),
                v2.mult(points[offset + 3], t * t  *t));
}

그리고 이렇게 곡선에 대한 일련의 점들을 생성할 수 있습니다.

function getPointsOnBezierCurve(points, offset, numPoints) {
  const cpoints = [];
  for (let i = 0; i < numPoints; ++i) {
    const t = i / (numPoints - 1);
    cpoints.push(getPointOnBezierCurve(points, offset, t));
  }
  return cpoints;
}

참고: v2.mult와 v2.add는 점들로 수식을 수행하는 데 유용하여 포함시킨 자바스크립트 함수입니다.

위 다이어그램에서 점의 개수를 선택할 수 있습니다. 곡선이 가파르면 더 많은 점을 필요로 할 겁니다. 곡선이 거의 직선이라면 더 적은 점을 필요로 할 겁니다. 한 가지 해결책은 곡선이 얼마나 휘었는지 확인하는 것인데요. 너무 휘었다면 2개의 곡선으로 나누면 됩니다.

나누는 부분은 간단합니다. 보간의 다양한 레벨을 다시 봐보면, 값 t에 대해 P1, Q1, R1, 빨간점은 곡선 하나를 만들고, 빨간점, R2, Q3, P4는 또 다른 곡선을 만듭니다. 즉 어디서든 곡선을 나눌 수 있고 원본과 일치하는 곡선 2개를 얻게 됩니다.

두 번째로 중요한 부분은 곡선을 분할해야 하는지 여부를 결정하는 겁니다. 인터넷을 둘러보다가 주어진 곡선이 얼마나 평평한지 결정하는 함수를 찾았습니다.

function flatness(points, offset) {
  const p1 = points[offset + 0];
  const p2 = points[offset + 1];
  const p3 = points[offset + 2];
  const p4 = points[offset + 3];

  let ux = 3 * p2[0] - 2 * p1[0] - p4[0]; ux *= ux;
  let uy = 3 * p2[1] - 2 * p1[1] - p4[1]; uy *= uy;
  let vx = 3 * p3[0] - 2 * p4[0] - p1[0]; vx *= vx;
  let vy = 3 * p3[1] - 2 * p4[1] - p1[1]; vy *= vy;

  if(ux < vx) {
    ux = vx;
  }

  if(uy < vy) {
    uy = vy;
  }

  return ux + uy;
}

이를 곡선의 점을 만드는 함수에 사용할 수 있습니다. 먼저 곡선이 너무 가파른지 확인합니다. 가파르면 세분화하고 아니라면 점을 추가할 겁니다.

function getPointsOnBezierCurveWithSplitting(points, offset, tolerance, newPoints) {
  const outPoints = newPoints || [];
  if (flatness(points, offset) < tolerance) {

    // 이 곡선의 끝점을 추가
    outPoints.push(points[offset + 0]);
    outPoints.push(points[offset + 3]);

  } else {

    // 세분화
    const t = .5;
    const p1 = points[offset + 0];
    const p2 = points[offset + 1];
    const p3 = points[offset + 2];
    const p4 = points[offset + 3];

    const q1 = v2.lerp(p1, p2, t);
    const q2 = v2.lerp(p2, p3, t);
    const q3 = v2.lerp(p3, p4, t);

    const r1 = v2.lerp(q1, q2, t);
    const r2 = v2.lerp(q2, q3, t);

    const red = v2.lerp(r1, r2, t);

    // 첫 번째 절반 수행
    getPointsOnBezierCurveWithSplitting([p1, q1, r1, red], 0, tolerance, outPoints);
    // 두 번째 절반 수행
    getPointsOnBezierCurveWithSplitting([red, r2, q3, p4], 0, tolerance, outPoints);

  }
  return outPoints;
}

이 알고리즘은 점이 충분한지 확인하는 데는 좋지만 불필요한 점을 제거하는 데는 그다지 좋지 않습니다.

이를 위해 인터넷에서 찾은 Ramer Douglas Peucker 알고리즘을 살펴봅시다.

알고리즘은 먼저 점 목록을 가져옵니다. 그리고 두 끝점으로 이루어진 선에서 가장 먼 점을 찾습니다. 그런 다음 해당 점이 선에서 일정 거리보다 더 멀리 있는지 확인합니다. 그 거리보다 더 가깝다면 두 끝점을 유지하고 나머지를 버립니다. 그렇지 않으면 시작점에서 가장 먼 지점까지 한 번, 그리고 가장 먼 지점에서 끝점까지 한 번 알고리즘을 다시 실행합니다.

function simplifyPoints(points, start, end, epsilon, newPoints) {
  const outPoints = newPoints || [];

  // 끝점에서 가장 먼 거리의 점을 찾습니다.
  const s = points[start];
  const e = points[end - 1];
  let maxDistSq = 0;
  let maxNdx = 1;
  for (let i = start + 1; i < end - 1; ++i) {
    const distSq = v2.distanceToSegmentSq(points[i], s, e);
    if (distSq > maxDistSq) {
      maxDistSq = distSq;
      maxNdx = i;
    }
  }

  // 해당 점이 너무 멀다면
  if (Math.sqrt(maxDistSq) > epsilon) {

    // 분할
    simplifyPoints(points, start, maxNdx + 1, epsilon, outPoints);
    simplifyPoints(points, maxNdx, end, epsilon, outPoints);

  } else {

    // 2개의 끝점 추가
    outPoints.push(s, e);
  }

  return outPoints;
}

v2.distanceToSegmentSq는 점에서 선분까지의 거리 제곱을 계산하는 함수인데요. 실제 거리보다 계산이 더 빠르기 때문에 거리 제곱을 사용합니다. 우리는 어느 지점이 가장 멀리 있는지만 알면 되기 때문에 거리 제곱은 실제 거리와 마찬가지로 잘 작동합니다.

다음은 실행중인 결과물입니다. 거리를 조절하여 더 많은 점들이 추가되거나 제거되는 걸 확인해보세요.

볼링핀으로 돌아와 봅시다. 우리는 위 코드를 전체 에디터로 확장할 수 있어야 합니다. 점을 추가하거나 제거할 수 있어야 하고, 제어점을 고정하거나 고정 해제할 수 있어야 합니다. 실행 취소 등도 필요하지만... 더 쉬운 방법이 있습니다. 위에서 언급한 주요 에디터를 사용하면 되는데요. 저는 이 온라인 에디터를 사용했습니다.

여기 제가 만든 볼링핀 SVG 실루엣입니다.

이는 4개의 베지에 곡선으로 만들어졌는데요. 해당 경로에 대한 데이터는 다음과 같습니다.

<path fill="none" stroke-width="5" d="
   m44,434
   c18,-33 19,-66 15,-111
   c-4,-45 -37,-104 -39,-132
   c-2,-28 11,-51 16,-81
   c5,-30 3,-63 -36,-63
"/>

데이터를 해석하면 이런 점들을 얻을 수 있습니다.

        ___
44, 371,   |
62, 338,   | 첫 번째 곡선
63, 305,___|__
59, 260,___|  |
55, 215,      | 두 번째 곡선
22, 156,______|__
20, 128,______|  |
18, 100,         | 세 번째 곡선
31,  77,_________|__
36,  47,_________|  |
41,  17,            | 네 번째 곡선
39, -16,            |
 0, -16,____________|

이제 곡선에 대한 데이터가 있으니 곡선 위의 점을 계산해야 합니다.

// 모든 부분에서 점을 가져옵니다.
function getPointsOnBezierCurves(points, tolerance) {
  const newPoints = [];
  const numSegments = (points.length - 1) / 3;
  for (let i = 0; i < numSegments; ++i) {
    const offset = i * 3;
    getPointsOnBezierCurveWithSplitting(points, offset, tolerance, newPoints);
  }
  return newPoints;
}

결과에 대해 simplifyPoints를 호출합니다.

이제 이것들을 회전시켜야 하는데요. 얼마나 많이 나눌지 결정하고, 각 분할에 대해 행렬 수학을 사용하여 Y축을 중심으로 점들을 회전시킵니다. 모든 점을 만들었으면 인덱스를 사용하여 삼각형으로 연결합니다.

// Y축을 중심으로 회전
function lathePoints(points,
                     startAngle,   // 시작하는 각도 (ie 0)
                     endAngle,     // 끝나는 각도 (ie Math.PI * 2)
                     numDivisions, // 만들 쿼드의 개수
                     capStart,     // true면 시작 부분을 막음
                     capEnd) {     // true면 끝 부분을 막음
  const positions = [];
  const texcoords = [];
  const indices = [];

  const vOffset = capStart ? 1 : 0;
  const pointsPerColumn = points.length + vOffset + (capEnd ? 1 : 0);
  const quadsDown = pointsPerColumn - 1;

  // 점 생성
  for (let division = 0; division <= numDivisions; ++division) {
    const u = division / numDivisions;
    const angle = lerp(startAngle, endAngle, u) % (Math.PI * 2);
    const mat = m4.yRotation(angle);
    if (capStart) {
      // 시작 시 Y축에 점 추가
      positions.push(0, points[0][1], 0);
      texcoords.push(u, 0);
    }
    points.forEach((p, ndx) => {
      const tp = m4.transformPoint(mat, [...p, 0]);
      positions.push(tp[0], tp[1], tp[2]);
      const v = (ndx + vOffset) / quadsDown;
      texcoords.push(u, v);
    });
    if (capEnd) {
      // 끝날 때 Y축에 점 추가
      positions.push(0, points[points.length - 1][1], 0);
      texcoords.push(u, 1);
    }
  }

  // 인덱스 생성
  for (let division = 0; division < numDivisions; ++division) {
    const column1Offset = division * pointsPerColumn;
    const column2Offset = column1Offset + pointsPerColumn;
    for (let quad = 0; quad < quadsDown; ++quad) {
      indices.push(column1Offset + quad, column2Offset + quad, column1Offset + quad + 1);
      indices.push(column1Offset + quad + 1, column2Offset + quad, column2Offset + quad + 1);
    }
  }

  return {
    position: positions,
    texcoord: texcoords,
    indices: indices,
  };
}

위 코드는 위치와 텍스처 좌표를 생성한 다음, 인덱스를 생성하여 삼각형을 만듭니다. capStart와 capEnd는 캡 포인트의 생성 여부를 지정합니다. 캔을 만들고 있다고 상상해보세요. 이러한 옵션으로 끝을 닫을지 여부를 지정할 겁니다.

간략화한 코드를 사용하여 다음과 같이 데이터로 WebGL 버퍼를 생성할 수 있습니다.

const tolerance = 0.15;
const distance = .4;
const divisions = 16;
const startAngle = 0;
const endAngle = Math.PI * 2;
const capStart = true;
const capEnd = true;

const tempPoints = getPointsOnBezierCurves(curvePoints, tolerance);
const points = simplifyPoints(tempPoints, 0, tempPoints.length, distance);
const arrays = lathePoints(points, startAngle, endAngle, divisions, capStart, capEnd);
const extents = getExtents(arrays.position);
if (!bufferInfo) {
  bufferInfo = webglUtils.createBufferInfoFromArrays(gl, arrays);

여기 예제가 있습니다.

슬라이더를 움직여서 결과에 어떻게 영향을 주는지 확인해보세요.

한 가지 문제가 있습니다. 삼각형을 활성화하면 텍스처가 고르게 적용되지 않는 것을 볼 수 있는데요. 이건 v 텍스처 좌표가 선에 있는 점의 인덱스를 기반으로 하기 때문입니다. 이들이 균등하게 간격을 둔다면 동작할 수도 있습니다. 하지만 그렇지 않기 때문에 다른 작업을 해야 합니다.

점을 순회하여 곡선의 총 길이와 곡선에 있는 각 점의 길이를 계산할 수 있는데요. 그런 다음 길이로 나누어 v에 대해 더 좋은 값을 구할 수 있습니다.

// Y 액세스를 중심으로 회전
function lathePoints(points,
                     startAngle,   // 시작하는 각도 (ie 0)
                     endAngle,     // 끝나는 각도 (ie Math.PI * 2)
                     numDivisions, // 만들 쿼드의 개수
                     capStart,     // true면 윗 부분을 막음
                     capEnd) {     // true면 아랫 부분을 막음
  const positions = [];
  const texcoords = [];
  const indices = [];

  const vOffset = capStart ? 1 : 0;
  const pointsPerColumn = points.length + vOffset + (capEnd ? 1 : 0);
  const quadsDown = pointsPerColumn - 1;

+  // v 좌표 생성
+  let vcoords = [];
+
+  // 먼저 점들의 길이를 계산합니다.
+  let length = 0;
+  for (let i = 0; i < points.length - 1; ++i) {
+    vcoords.push(length);
+    length += v2.distance(points[i], points[i + 1]);
+  }
+  vcoords.push(length);  // 마지막 점
+
+  // 이제 각각을 전체 길이로 나눕니다.
+  vcoords = vcoords.map(v => v / length);

  // 점 생성
  for (let division = 0; division <= numDivisions; ++division) {
    const u = division / numDivisions;
    const angle = lerp(startAngle, endAngle, u) % (Math.PI * 2);
    const mat = m4.yRotation(angle);
    if (capStart) {
      // 시작 시 Y축에 점 추가
      positions.push(0, points[0][1], 0);
      texcoords.push(u, 0);
    }
    points.forEach((p, ndx) => {
      const tp = m4.transformPoint(mat, [...p, 0]);
      positions.push(tp[0], tp[1], tp[2]);
*      texcoords.push(u, vcoords[ndx]);
    });
    if (capEnd) {
      // 끝날 때 Y축에 점 추가
      positions.push(0, points[points.length - 1][1], 0);
      texcoords.push(u, 1);
    }
  }

  // 인덱스 생성
  for (let division = 0; division < numDivisions; ++division) {
    const column1Offset = division * pointsPerColumn;
    const column2Offset = column1Offset + pointsPerColumn;
    for (let quad = 0; quad < quadsDown; ++quad) {
      indices.push(column1Offset + quad, column1Offset + quad + 1, column2Offset + quad);
      indices.push(column1Offset + quad + 1, column2Offset + quad + 1, column2Offset + quad);
    }
  }

  return {
    position: positions,
    texcoord: texcoords,
    indices: indices,
  };
}

그리고 여기 결과입니다.

이 텍스처 좌표들은 아직 완벽하지 않습니다. 캡에 대해 무엇을 할지 정하지 않았는데요. 이게 바로 모델링 프로그램을 써야하는 또 다른 이유입니다. 캡에 대한 UV 좌표를 계산하는 다른 아이디어를 생각해볼 수 있겠지만 그다지 유용하진 않을 겁니다. 구글에 배럴 UV 매핑이라고 검색해보면 완벽한 UV 좌표를 얻는 것이, 데이터 입력 문제 정도의 수학 문제가 아니며, 해당 데이터를 입력하기 위해 좋은 도구가 필요하다는 것을 알 수 있습니다.

우리가 해야할 또 다른 것이 있는데 바로 법선을 추가하는 겁니다.

곡선의 각 점에 대한 법선을 계산할 수 있는데요. 실제로 이 페이지의 예제로 돌아가보면 R1과 R2로 구성된 선이 곡선의 접선입니다.

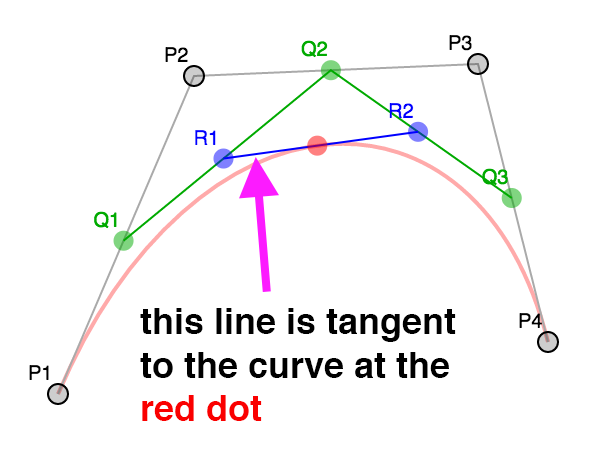
법선은 접선에 수직이므로 접선을 사용하면 쉽게 법선을 생성할 수 있을 겁니다

하지만 다음과 같은 실루엣의 촛대를 만들고 싶다고 상상해봅시다.

매끄러운 부분도 많지만 각진 부분도 많습니다. 사용할 법선을 어떻게 정해야 할까요? 설상가상으로 뾰족한 모서리가 필요할 때 추가 정점을 필요로 하는데요. 정점은 위치과 법선을 가지기 때문에 같은 위치에 대해 다른 법선이 필요하다면 다른 정점이 필요합니다. 이게 큐브를 만들 때 실제로 최소 24개의 정점이 필요한 이유입니다. 큐브의 모서리는 8개뿐이지만 큐브의 각 면은 모서리에 서로 다른 법선을 필요로 합니다.

큐브를 생성할 때 법선을 생성하는 것은 쉽지만 좀 더 복잡한 모양의 경우 선택할 수 있는 쉬운 방법은 없습니다.

모든 모델링 프로그램은 법선을 생성하는 다양한 옵션을 가집니다. 일반적인 방법은 모든 단일 정점에 대해 해당 정점을 공유하는 모든 폴리곤의 법선을 평균화하는 겁니다. 단, 사용자가 최대 각도를 선택할 수 있습니다. 정점으로 공유된 폴리곤 사이의 각도가 최대 각도보다 크면 새로운 정점을 생성합니다.

한 번 해봅시다.

function generateNormals(arrays, maxAngle) {
  const positions = arrays.position;
  const texcoords = arrays.texcoord;

  // 먼저 각 면의 법선을 계산합니다.
  let getNextIndex = makeIndiceIterator(arrays);
  const numFaceVerts = getNextIndex.numElements;
  const numVerts = arrays.position.length;
  const numFaces = numFaceVerts / 3;
  const faceNormals = [];

  // 모든 면에 대한 법선을 계산합니다.
  // 그동안 모든 면의 정점에 대해 새로운 정점을 만듭니다.
  for (let i = 0; i < numFaces; ++i) {
    const n1 = getNextIndex() * 3;
    const n2 = getNextIndex() * 3;
    const n3 = getNextIndex() * 3;

    const v1 = positions.slice(n1, n1 + 3);
    const v2 = positions.slice(n2, n2 + 3);
    const v3 = positions.slice(n3, n3 + 3);

    faceNormals.push(m4.normalize(m4.cross(m4.subtractVectors(v1, v2), m4.subtractVectors(v3, v2))));
  }

  let tempVerts = {};
  let tempVertNdx = 0;

  // 이는 정점 위치가 정확히 일치한다고 가정합니다.

  function getVertIndex(x, y, z) {

    const vertId = x + "," + y + "," + z;
    const ndx = tempVerts[vertId];
    if (ndx !== undefined) {
      return ndx;
    }
    const newNdx = tempVertNdx++;
    tempVerts[vertId] = newNdx;
    return newNdx;
  }

  // 공유된 정점을 파악해야 하는데요.
  // 이는 면(삼각형)을 보는 것만큼 간단하지 않습니다.
  // 예를 들어 표준 원기둥이 있다면,
  //
  //
  //      3-4
  //     /   \
  //    2     5   S에서 시작하여 E로 돌아가는 원기둥을 내려다보면,
  //    |     |   E와 S는 UV 좌표를 공유하지 않기 때문에
  //    1     6   우리가 가진 데이터에서 같은 정점이 아닙니다.
  //     \   /    
  //      S/E
  //
  // 시작과 끝 정점은 다른 UV를 가지기 때문에 정점을 공유하지 않지만
  // 정점을 공유하는 것으로 간주하지 않으면 잘못된 법선을 얻게 됩니다.

  const vertIndices = [];
  for (let i = 0; i < numVerts; ++i) {
    const offset = i * 3;
    const vert = positions.slice(offset, offset + 3);
    vertIndices.push(getVertIndex(vert));
  }

  // 모든 정점을 살펴보고 어느 면이 있는지 기록합니다.
  const vertFaces = [];
  getNextIndex.reset();
  for (let i = 0; i < numFaces; ++i) {
    for (let j = 0; j < 3; ++j) {
      const ndx = getNextIndex();
      const sharedNdx = vertIndices[ndx];
      let faces = vertFaces[sharedNdx];
      if (!faces) {
        faces = [];
        vertFaces[sharedNdx] = faces;
      }
      faces.push(i);
    }
  }

  // 이제 모든 면을 살펴보고 면의 각 정점에 대한 법선을 계산합니다.
  // maxAngle 차이보다 크지 않은 면만 포함합니다.
  // newPositions, newTexcoords, newNormals 배열에 결과를 추가하고, 동일한 정점은 모두 버립니다.
  tempVerts = {};
  tempVertNdx = 0;
  const newPositions = [];
  const newTexcoords = [];
  const newNormals = [];

  function getNewVertIndex(x, y, z, nx, ny, nz, u, v) {
    const vertId =
        x + "," + y + "," + z + "," +
        nx + "," + ny + "," + nz + "," +
        u + "," + v;

    const ndx = tempVerts[vertId];
    if (ndx !== undefined) {
      return ndx;
    }
    const newNdx = tempVertNdx++;
    tempVerts[vertId] = newNdx;
    newPositions.push(x, y, z);
    newNormals.push(nx, ny, nz);
    newTexcoords.push(u, v);
    return newNdx;
  }

  const newVertIndices = [];
  getNextIndex.reset();
  const maxAngleCos = Math.cos(maxAngle);
  // 각 면마다
  for (let i = 0; i < numFaces; ++i) {
    // 이 면에 대한 법선 가져오기
    const thisFaceNormal = faceNormals[i];
    // 면의 각 정점마다
    for (let j = 0; j < 3; ++j) {
      const ndx = getNextIndex();
      const sharedNdx = vertIndices[ndx];
      const faces = vertFaces[sharedNdx];
      const norm = [0, 0, 0];
      faces.forEach(faceNdx => {
        // 이 면이 같은 방향을 향하는지 여부
        const otherFaceNormal = faceNormals[faceNdx];
        const dot = m4.dot(thisFaceNormal, otherFaceNormal);
        if (dot > maxAngleCos) {
          m4.addVectors(norm, otherFaceNormal, norm);
        }
      });
      m4.normalize(norm, norm);
      const poffset = ndx * 3;
      const toffset = ndx * 2;
      newVertIndices.push(getNewVertIndex(
          positions[poffset + 0], positions[poffset + 1], positions[poffset + 2],
          norm[0], norm[1], norm[2],
          texcoords[toffset + 0], texcoords[toffset + 1]));
    }
  }

  return {
    position: newPositions,
    texcoord: newTexcoords,
    normal: newNormals,
    indices: newVertIndices,
  };

}

function makeIndexedIndicesFn(arrays) {
  const indices = arrays.indices;
  let ndx = 0;
  const fn = function() {
    return indices[ndx++];
  };
  fn.reset = function() {
    ndx = 0;
  };
  fn.numElements = indices.length;
  return fn;
}

function makeUnindexedIndicesFn(arrays) {
  let ndx = 0;
  const fn = function() {
    return ndx++;
  };
  fn.reset = function() {
    ndx = 0;
  }
  fn.numElements = arrays.positions.length / 3;
  return fn;
}

function makeIndiceIterator(arrays) {
  return arrays.indices
      ? makeIndexedIndicesFn(arrays)
      : makeUnindexedIndicesFn(arrays);
}

위 코드에서 먼저 원본 점으로부터 각 면(각 삼각형)에 대한 법선을 생성합니다. 그런 다음 정점 인덱스 세트를 생성하여 동일한 점을 찾는데요. 그 이유는 점을 회전할 때 첫 번째 점과 마지막 점이 일치해야 하지만 다른 UV 좌표를 가지므로 같은 점이 아니기 때문입니다. 정점 법선을 계산하려면 같은 점으로 간주되어야 합니다.

완료되면 각 정점에 대해 사용되는 모든 면의 목록을 만듭니다.

마지막으로 maxAngle보다 큰 것들을 제외하고 각 정점이 사용하는 모든 면의 법선을 평균화하여 새로운 정점 세트를 생성합니다.

여기 결과입니다.

원하는 곳에 뾰족한 모서리를 만들었습니다. maxAngle을 더 크게 만들면 인접한 면들이 법선 계산에 포함되기 시작할 때 모서리가 매끄러워지는 것을 볼 수 있습니다. 또한 divisions를 5나 6으로 조정한 다음 주변 가장자리가 딱딱하지만 원하는 부분은 부드러워질 때까지 maxAngle을 조정해보세요. mode를 lit으로 설정하여 법선이 필요한 이유인 조명과 함께 객체가 어떻게 보이는지 확인할 수도 있습니다.

그래서 무엇을 배웠나요?

3D 데이터를 만들고 싶다면 3D 모델링 패키지를 사용하면 된다는 걸 배웠습니다!!! 😝

정말로 유용한 무언가를 하려면 실제 UV 에디터가 필요할 겁니다. 캡을 잘 다루는 것도 3D 에디터가 도움을 줄 수 있습니다. 선반 처리할 때 제한된 옵션 세트를 사용하는 대신에 에디터의 다른 기능을 사용하여 캡을 추가하고 더 쉽게 캡에 대한 UV를 생성할 수 있습니다. 또한 3D 에디터는 Extrude Face와 Extrude Along Path를 지원하는데, 위의 선반 처리 예제를 보면 어떻게 작동하는지 알 수 있습니다.

참고

베지에 곡선에 대한 멋진 페이지가 없었다면 이걸 완료할 수 없었다고 언급하고 싶습니다.

나머지 연산자는 여기서 뭘 하는 건가요?

lathePoints 함수를 자세히 보면 각도를 계산할 때 나머지 연산을 볼 수 있습니다.

for (let division = 0; division <= numDivisions; ++division) {
  const u = division / numDivisions;
*  const angle = lerp(startAngle, endAngle, u) % (Math.PI * 2);

왜 저기에 있나요?

원을 중심으로 점을 회전할 때 첫 번째와 마지막 점이 일치하도록 하고 싶어서 입니다. Math.sin(0)과 Math.sin(Math.PI * 2)는 일치해야 하지만 컴퓨터의 부동 소수점 계산은 완벽하지 않으며 충분히 가깝지만 일반적으로 100% 동일하지는 않습니다.

이는 법선을 계산하려고 할 때 중요합니다. 우리는 정점이 사용하는 모든 면을 알려고 하는데요. 정점을 비교하여 이를 계산합니다. 만약 2개의 정점이 같다면 같은 정점이라고 가정합니다. 하지만 Math.sin(0)과 Math.sin(Math.PI * 2)가 같지 않기 때문에 동일한 정점으로 간주되지 않습니다. 이는 법선을 계산할 때 모든 면을 고려하지 않고 법선들이 잘못 나타남을 의미합니다.

여기 그런 일이 일어났을 때의 결과입니다.

보다시피 정점이 100% 일치하지 않기 때문에 공유된 것으로 간주되지 않는 곳에 경계선이 생깁니다.

첫 생각은 일치하는 정점을 확인할 때 일정 거리 내에 있는지 확인하도록 수정해야 한다는 겁니다. 그렇다면 같은 정점인거죠. 예를 들어 이렇게 할 수 있습니다.

const epsilon = 0.0001;
const tempVerts = [];
function getVertIndex(position) {
  if (tempVerts.length) {
    // 가장 가까이 존재하는 정점 찾기
    let closestNdx = 0;
    let closestDistSq = v2.distanceSq(position, tempVerts[0]);
    for (let i = 1; i < tempVerts.length; ++i) {
      let distSq = v2.distanceSq(position, tempVerts[i]);
      if (distSq < closestDistSq) {
        closestDistSq = distSq;
        closestNdx = i;
      }
    }
    // 가장 가까운 정점은 충분히 가까운가?
    if (closestDistSq < epsilon) {
      // 그렇다면 정점의 인덱스 반환
      return closestNdx;
    }
  }
  // 일치하지 않으면 새로운 정점을 추가하고 해당 인덱스를 반환
  tempVerts.push(position);
  return tempVerts.length - 1;
}

효과가 있었습니다! 경계선이 없어졌네요. 하지만 실행에 몇 초가 걸리고 인터페이스를 사용할 수 없게 되었습니다. 이는 O^2 해결법이기 때문인데요. distance는 낮고, divisions은 높게, 최대 정점에 관한 슬라이더를 움직여보면, 정점을 114000개까지 생성할 수 있습니다. O^2일 경우 최대 12조에 가까운 반복이 발생합니다.

인터넷에서 쉬운 해결책을 찾아봤지만 찾지 못했습니다. 일치하는 점을 더 빨리 찾도록 만들기 위해 모든 점을 팔진트리에 넣는 걸 생각해봤지만 이 글에서 다루긴 너무 많은 것 같습니다.

그제서야 끝점만 문제라면 수식에 나머지 연산을 추가하여 실제로 점이 동일하도록 할 수 있다는 것을 깨달았습니다. 원본 코드는 이렇습니다.

  const angle = lerp(startAngle, endAngle, u);

그리고 새로운 코드는 이렇습니다.

  const angle = lerp(startAngle, endAngle, u) % (Math.PI * 2);

나머지 연산 덕분에 endAngle이 Math.PI * 2일 때 angle은 0이 되고 이는 startAngle과 동일합니다. 경계선이 없어졌네요. 문제가 해결되었습니다!

그래도 여전히 distance를 0.001로 divisions를 60으로 설정하면 메시를 다시 계산하는 데 거의 1초가 걸립니다. 이를 최적화하는 방법이 있을 수도 있지만 복잡한 메시를 생성하는 게 일반적으로 느린 작업이라는 것을 깨닫는 게 요점이라고 생각합니다. 이게 3D 게임은 60fps로 실행할 수 있지만 3D 모델링 패키지는 종종 매우 낮은 프레임 레이트로 작동하는 이유입니다.

const mat = m4.yRotation(angle);
...
points.forEach((p, ndx) => {
  const tp = m4.transformPoint(mat, [...p, 0]);
  ...

const s = Math.sin(angle);
const c = Math.cos(angle);
...
points.forEach((p, ndx) => {
  const x = p[0];
  const y = p[1];
  const z = p[2];
  const tp = [
    x * c - z * s,
    y,
    x * s + z * c,
  ];
  ...

   const mat = m4.axisRotation(userSuppliedAxis, angle);