この記事はWebGLシリーズの一つである。最初の記事はWebGLの基本で始まった。 そして、前回の記事は正投影についてだった。まだ読んでいなかったら先に読んで下さい。

前回の記事は、三次元の描画のし方についてだったが、その方法では遠近法がなかった。その記事のサンプルは正投影を使ったが、 「三次元で何かを描画したい」と思った人の想像と違うだろう。

そこで遠近法を追加しなければいけない。遠近法は何だろう？遠近法は遠ければ遠くほど小さく見えることである。

上記の絵を見たら遠い物が小さく書かれている。 前回のサンプルで遠い物を小さく描画させたければ、クリップ空間のXとY値をZで割ることで出来るだろう。

このように考えてみよう。10,15から20,15の線とする。前回のサンプルで描画したら、その線の横は１０単位になる。 Zで割って、Z=1なら

10 / 1 = 10
20 / 1 = 20
abs(10-20) = 10

その線は１０ピクセルになる。Z=2なら

10 / 2 = 5
20 / 2 = 10
abs(5 - 10) = 5

横は５ピクセルになる。Z=3なら

10 / 3 = 3.333
20 / 3 = 6.666
abs(3.333 - 6.666) = 3.333

横は3.333になる。

Zが大きければ大きいほど、つまり、遠ければ遠くほど小さく描かれる。 クリップ空間でZが+1〜-1になるので簡単にZで割れる。 Zは補正係数を掛けると調整出来るようになる。

じゃあ、やってみょう！最初に頂点シェーダーを更新して、頂点位置を補正係数に掛けたZで割る。

<script id="vertex-shader-3d" type="x-shader/x-vertex">
...
+uniform float u_fudgeFactor;  // 補正係数
...
void main() {
  // positionを行列に掛ける。
  vec4 position = u_matrix * a_position;

+  // ｚで割る値を調整する。
+  float zToDivideBy = 1.0 + position.z * u_fudgeFactor;

*  // XとYをZで割る。
*  gl_Position = vec4(position.xy / zToDivideBy, position.zw);

　　...
}
</script>

クリップ空間のZが-1〜+1なので、１を足して、zToDivideByは0〜+2*fudgeFactorになる。

fudgeFactorを設定出来るように更新しなきゃ。

  ...
  var fudgeLocation = gl.getUniformLocation(program, "u_fudgeFactor");

  ...
  var fudgeFactor = 1;
  ...
  function drawScene() {
    ...
    // fudgeFactorを設定する。
    gl.uniform1f(fudgeLocation, fudgeFactor);

    // 図形を描画する。
    var primitiveType = gl.TRIANGLES;
    var offset = 0;
    var count = 16 * 6;
    gl.drawArrays(primitiveType, offset, count);

そしてこの結果になる。

分からなければ、「fudgeFactor」のスライダを操作して、1.0から0.0にすると、前と同じようにZで割ってない形になる。

実は、WebGLがgl_Positionを割り当てた値を自動的にWで割っている。

簡単に確認したければ、頂点シェーダーで手動でXとYを割る代わりにgl_Position.wをzToDivideByに割り当てる。

<script id="vertex-shader-2d" type="x-shader/x-vertex">
...
uniform float u_fudgeFactor;
...
void main() {
  // positionを行列に掛ける。
  vec4 position = u_matrix * a_position;

  // ｚで割る値を調整する。
  float zToDivideBy = 1.0 + position.z * u_fudgeFactor;

*  // XとYをZで割る。
*  gl_Position = vec4(position.xyz, zToDivideBy);

  // 色をピクセルシェーダーに渡す。
  v_color = a_color;
}
</script>

これは前と全く同じ結果になる。

なぜWebGLが自動的にWで割と便利なのか？そうなると魔法のような行列数学でZをWに移動出来るからだ。

このような行列を使えば。。。

1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 1,
0, 0, 0, 0,

ZがWに移動される。縦の行ごとにみて。。。

x_out = x_in * 1 +
        y_in * 0 +
        z_in * 0 +
        w_in * 0 ;

y_out = x_in * 0 +
        y_in * 1 +
        z_in * 0 +
        w_in * 0 ;

z_out = x_in * 0 +
        y_in * 0 +
        z_in * 1 +
        w_in * 0 ;

w_out = x_in * 0 +
        y_in * 0 +
        z_in * 1 +
        w_in * 0 ;

単純化すると。。。

x_out = x_in;
y_out = y_in;
z_out = z_in;
w_out = z_in;

w_inはいつも１になっているので、シェーダーと同じように１を足すことも出来る。

1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 1,
0, 0, 0, 1,

それでw_outの計算式がこうなる。

w_out = x_in * 0 +
        y_in * 0 +
        z_in * 1 +
        w_in * 1 ;

いつもw_in=1.0なので実はこうなる。

w_out = z_in + 1;

最後に補正係数のfudgeFactorに掛けることも追加出来る。

1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, fudgeFactor,
0, 0, 0, 1,

という意味はこれ

w_out = x_in * 0 +
        y_in * 0 +
        z_in * fudgeFactor +
        w_in * 1 ;

単純化すると

w_out = z_in * fudgeFactor + 1;

さあ、また行列しか使ってない形に戻そう。

まず頂点シェーダーを前の単純な形に戻す。

<script id="vertex-shader-2d" type="x-shader/x-vertex">
uniform mat4 u_matrix;

void main() {
  // positionを行列に掛ける。
  gl_Position = u_matrix * a_position;
  ...
}
</script>

次に、Z → Wの行列作成関数を作ろう。

function makeZToWMatrix(fudgeFactor) {
  return [
    1, 0, 0, 0,
    0, 1, 0, 0,
    0, 0, 1, fudgeFactor,
    0, 0, 0, 1,
  ];
}

そして、その行列を含むように更新する。

    ...
    // Compute the matrices
*    var matrix = makeZToWMatrix(fudgeFactor);
*    matrix = m4.multiply(matrix, m4.projection(gl.canvas.clientWidth, gl.canvas.clientHeight, 400));
    matrix = m4.translate(matrix, translation[0], translation[1], translation[2]);
    matrix = m4.xRotate(matrix, rotation[0]);
    matrix = m4.yRotate(matrix, rotation[1]);
    matrix = m4.zRotate(matrix, rotation[2]);
    matrix = m4.scale(matrix, scale[0], scale[1], scale[2]);

    ...

また結果は全く同じである。

上記を見せたのは、WebGLが自動的にWで割っているので、頂点を補正係数に掛けたZで割りたければ、 行列しか要らないことを説明しかったからだ。

でもまだ色々な問題が残っている。例えばZを-100ぐらいにすればこのような結果になる。

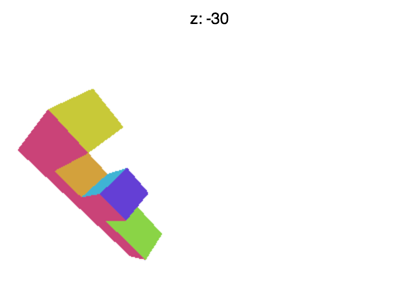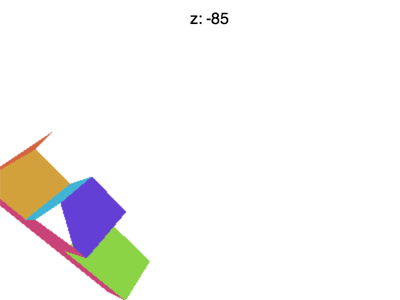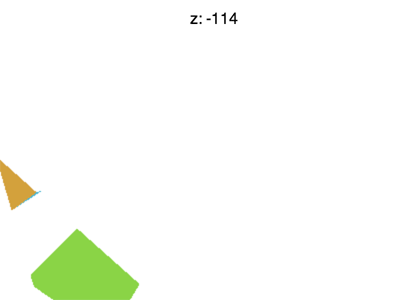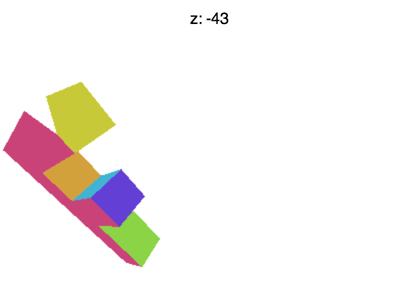
それは何でだろう？何で「F」が消えているか？XとYは-1〜+1の制限があると同じようにZも-1〜+1の制限がある。 この消えているところはZが−１以下になっている場合である。

その問題を解決する数学を細かく説明出来るけど、二次元の投影行列数学と同じように答えを導き出すこと出来るだろう。Zをとって、何かを足して、何かにスケールすると、 どの値の範囲からも-1〜+1出来る。

それら全部を一つの行列で出来る。その上、補正係数のfudgeFactorはfieldOfViewという視野も同じ行列で決められる。

これはその行列の関数である。

var m4 = {
  perspective: function(fieldOfViewInRadians, aspect, near, far) {
    var f = Math.tan(Math.PI * 0.5 - 0.5 * fieldOfViewInRadians);
    var rangeInv = 1.0 / (near - far);

    return [
      f / aspect, 0, 0, 0,
      0, f, 0, 0,
      0, 0, (near + far) * rangeInv, -1,
      0, 0, near * far * rangeInv * 2, 0
    ];
  },

  ...

この行列で全ての変換が出来る。三次元単位はクリップ空間にする。好きな視野、 好きなZ空間にもする。目、またカメラは0,0,0にあるとする。zNearというZの近い境界とfieldOfViewの視野で Z=-zNearの頂点のZは-1になって、中心点からfieldOfViewの上半分と下半分の頂点のYはそれぞれ+1か-1になる。頂点のX はaspectというキャンバスの比較率で計算する。最後に、Zが-zFarの頂点はZ = 1になる。

この行列の働き方のダイヤグラムである。

このトップがない四角錐は錘台(すいだい）と呼ばれる。この行列はその錘台の空間からクリップ空間に変換する。 zNearは前面を定義して、zFarは裏面を定義する。zNearを23にすると回転している立方体がクリップされる。 zFarを24にすると立方体の後ろの方がクリップされることも見える。

あと一つだけ問題が残っている。この行列は原点(0,0,0)から-Zの方に上は＋Yで見ている。今までの投影行列と違う。 この行列を使う為に図形をビューの前に移動しなければいけない。

「F」を移動したらいい。前は45,150,0だったが、-150,0,-360を移動しよう。

前はm4.projectionを呼び出したが、今回m4.perspectiveを呼び出す。

var aspect = gl.canvas.clientWidth / gl.canvas.clientHeight;
var zNear = 1;
var zFar = 2000;
var matrix = m4.perspective(fieldOfViewRadians, aspect, zNear, zFar);
matrix = m4.translate(matrix, translation[0], translation[1], translation[2]);
matrix = m4.xRotate(matrix, rotation[0]);
matrix = m4.yRotate(matrix, rotation[1]);
matrix = m4.zRotate(matrix, rotation[2]);
matrix = m4.scale(matrix, scale[0], scale[1], scale[2]);

そしてこうなる。

頂点を行列に掛けるだけの形に戻った。それだけでZの空間と視野も選べるようになった。 まだ完成してないけどこの記事も多大部長くなってきた。次に、カメラである。