本記事もWebGLシリーズの一つである。最初の記事はWebGLの基本で、そして前回の記事は二次元で移動することについての記事である.

まず、上手く説明出来るかどうか分からないが、ベストを尽くしてみよう。

最初に「単位円」というものを紹介したいと思う。中学校で学んだ数学を思い出せば、 円形には半径がある(そこ！簡単すぎるからといって寝てしまわないで！)。 円形の半径は円の中心点から円周までの距離である。 「単位円」は半径を1.0とした円である。

これは単位円である。

上の図で、青いハンドルを操作したらXとYの値が変わることに注目して下さい。 それは円周上の位置を表している。 真上はYが1.0でXが0.0である。真右ならXが1.0でYが0.0になる。

小学校の数学を思い出せば、何かに1を掛けるとその数字と同じになる。例えば123ｘ1＝123である。 それは結構常識であるだろう？単位円はこの「１」と似たものだ。半径が１の円であり、言うなればある種の「１」だ。 それは「回転する１」である。「何かに１を掛ける」と「同じ数字になる」ように、「何かに単位円を掛ける」と「魔法のように回転する」。

前回のサンプルの図形頂点を単位円のXとYに掛けよう！

これは更新された頂点シェーダーである。

<script id="vertex-shader-2d" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
+uniform vec2 u_rotation;  // 単位円の円周上の位置座標

void main() {
+  // 座標を回転する
+  vec2 rotatedPosition = vec2(
+     a_position.x * u_rotation.y + a_position.y * u_rotation.x,
+     a_position.y * u_rotation.y - a_position.x * u_rotation.x);

  // 移動距離を足す
*  vec2 position = rotatedPosition + u_translation;

そしてJavaScriptをその２つの値を設定出来るように更新する。

  ...

+  var rotationLocation = gl.getUniformLocation(program, "u_rotation");

  ...

+  var rotation = [0, 1];

  ...

  // シーンを描画する。
  function drawScene() {

    ...

    // 移動距離を設定する。
    gl.uniform2fv(translationLocation, translation);

+    // 回転角を設定する。
+    gl.uniform2fv(rotationLocation, rotation);

    // 図形を描画する。
    var primitiveType = gl.TRIANGLES;
    var offset = 0;
    var count = 18;  // ６つの三角形、三角形ごとに３頂点
    gl.drawArrays(primitiveType, offset, count);
  }

そしてこれがその結果である。単位円のハンドルを操作して回転、 スライダを使って移動してみよう。

何でこういう結果が出るか？よろしい、計算式を見て下さい。

rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;

回転したい四角形があることを想像しよう。回転する前は右上の頂点は(3.0, 9.0)である。 単位円の円周上、真上から右回り30度の位置を選ぼう。

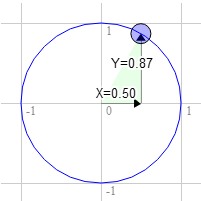
この、単位円の円周上の位置は(0.50, 0.87)である。

   3.0 * 0.87 + 9.0 * 0.50 = 7.1
   9.0 * 0.87 - 3.0 * 0.50 = 6.3

これが回転する為に必要な値になってくる！

60度も同じようにしてみよう。

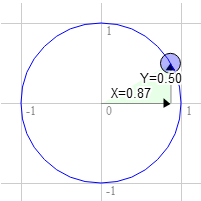
この、単位円の円周上の位置は(0.87, 0.50)

   3.0 * 0.50 + 9.0 * 0.87 = 9.3
   9.0 * 0.50 - 3.0 * 0.87 = 1.9

この、単位円の円周上の位置を右回りに移動するとXが大きくなって、Yが小さくなって行く。90度を過ぎたら Xが小さくなって、Yが大きくなって行く。そのパターンで回転出来る。

「単位円の円周上の位置」には別の名前がある。 それは正弦(sine)と余弦(cosine)と呼ばれている。 どんな角度でもその角度の正弦と余弦はこのように調べられる。

function printSineAndCosineForAnAngle(angleInDegrees) {
  var angleInRadians = angleInDegrees * Math.PI / 180;
  var s = Math.sin(angleInRadians);
  var c = Math.cos(angleInRadians);
  console.log("s = " + s + " c = " + c);
}

このコードをJavaScriptコンーソルにコピー＆ペーストして、そして printSineAndCosineForAngle(30)を入力したらs = 0.49 c = 0.87が 表示される(note:値は四捨五入した)。

これらを組み合わせたら、どんな図形をどんな角度にでも回転出来るようになる。 rotationを希望の角度の正弦と余弦に設定するだけである.

  ...
  var angleInRadians = angleInDegrees * Math.PI / 180;
  rotation[0] = Math.sin(angleInRadians);
  rotation[1] = Math.cos(angleInRadians);

これは角度しか使わない版である。移動と回転するためにスライダを操作してみよう。

ここまで良い説明だったかな〜。。。 これは一般的な回転する方法じゃないのでまだ読み続けて下さい。 ２つ後の記事でそれにたどり着く。次はもっと簡単なこと、拡大と縮小のやり方である。