Cet article est la suite d'une série de posts consacrés à WebGL. Le premier présentait les bases et le précédent parlait des translations. Si vous ne les avez pas lus vous préférez peut-être y jeter un oeil d'abord.

Je vais commencer par admettre directement que je n'ai aucune idée si ça va avoir du sens mais hé, autant essayer. D'abord je voudrais introduire la notion de cercle trigonométrique ou cercle unitaire. Si vous vous rappelez les bons vieux cours de maths de collège (c'est bon ne vous endormez pas !) un cercle a un rayon. Ce rayon est la distance du centre jusqu'au bord du cercle. Un cercle unitaire a un rayon de distance 1.

Voilà un cercle trigonométrique.

Notez que si vous déplacez le bouton bleu autour du cercle les coordonnées x et y changent. Elles représentent la position du point sur le cercle. Tout en haut Y vaut 1 et X vaut 0. Sur la droite X vaut 1 et Y vaut 0.

Si vous vous souvenez de cours autour de la classe de CE1 vous savez que ce qu'on multiplie par 1 reste pareil : 123 * 1 = 123. Plutôt simple n'est-ce pas ? Hé bien un cercle trigonométrique, avec un rayon de 1, est aussi une forme de 1. C'est un 1 qui tourne. Donc on peut multiplier quelque chose par ce cercle unitaire, et d'une certaine façon c'est comme multiplier par 1, sauf qu'en plus deux trois trucs se passent et ça tourne :)

On va prendre ces valeurs X et Y de n'importe quel point sur le cercle trigonométrique et on va multiplier notre géométrie avec elles depuis notre exemple précédent.

Voilà le nouveau shader

<script id="shader-de-vertex-2d" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;

void main() {
  // Tourne
  vec2 positionTournee = vec2(
     a_position.x * u_rotation.y + a_position.y * u_rotation.x,
     a_position.y * u_rotation.y - a_position.x * u_rotation.x);

  // Ajoute la translation
  vec2 position = positionTournee + u_translation;

Et on change le javascript pour envoyer ces deux valeurs :

  ...
  var emplacementRotation = gl.getUniformLocation(programme, "u_rotation");
  ...
  var rotation = [0, 1];
  ..
  // Rend la scène.
  function rendreScene() {
    // Efface le canvas
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Transmets les valeurs de translation au programme actif
    gl.uniform2fv(emplacementTranslation, translation);

    // Transmets les valeurs de rotation au programme actif
    gl.uniform2fv(emplacementRotation, rotation);

    // Appel de rendu
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Voilà le résultat. Bougez le bouton sur le cercle pour tourner ou déplacer.

Pourquoi ça fonctionne ? Regardez les opérations :

rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;

Disons que vous avez un rectangle et que vous voulez le tourner. Avant, le coin en haut à droite est à (3,9). Choisissons un point sur le cercle qui soit à 30 degrés plus loin dans le sens des aiguilles d'une montre, depuis disons, midi.

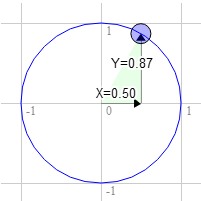
La position sur le cercle ici est à (0.50,0.87)

   3.0 * 0.87 + 9.0 * 0.50 = 7.1
   9.0 * 0.87 - 3.0 * 0.50 = 6.3

Exctement ce qu'on voulait

Pour 60 degrees dans le même sens

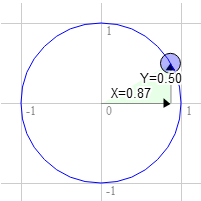
La position sur le cercle est (0.87,0.50).

   3.0 * 0.50 + 9.0 * 0.87 = 9.3
   9.0 * 0.50 - 3.0 * 0.87 = 1.9

Vous voyez que pendant qu'on bouge le point dans le sens des aiguilles d'une montre X devient plus grand et Y plus petit. Si on dépasse 90 degrés X deviendrait plus petit et Y redeviendrait plus grand. C'est ce qui nous donne la rotation.

Il y a un autre nom pour les points sur un cercle trigonométrique. On les appelle sinus et cosinus. Pour n'importe quel angle on peut juste regarder le sinus et le cosinus comme ceci :

function indiqueSinusEtCosinusPourLAngle(angleEnDegres) {
  var angleEnRadians = angleEnDegres * Math.PI / 180;
  var s = Math.sin(angleEnRadians);
  var c = Math.cos(angleEnRadians);
  console.log("s = " + s + " c = " + c);
}

Si vous copiez et collez ce code dans la console du navigateur et tapez indiqueSinusEtCosinusPourLAngle(30) vous verrez qu'il indique s = 0.49 c = 0.87 (note: j'ai arrondi les nombres).

Si vous mettez tout ça ensemble vous pouvez tourner votre géométrie de n'importe quel angle. Mettez juste les valeurs de sinus et de cosinus de l'angle de rotation que vous voulez.

  ...
  var angleEnRadians = angleEnDegres * Math.PI / 180;
  rotation[0] = Math.sin(angleEnRadians);
  rotation[1] = Math.cos(angleEnRadians);

Voici une version qui a juste un changement d'angle. Bougez les sliders pour déplacer ou tourner.

J'espère que c'était utile. Plus facile pour la suite : les changements d'échelle.