Tekst jest kontynuacją serii poświęconej WebGL. Pierwszy artykuł rozpoczynał od podstaw, a poprzedni opisywał przesunięcia geometryczne.

Przyznaję się szczerze, że nie mam pomysłu jak dobrze wyjaśnić kwestię obrotów, ale spróbuję. Na wstępie chciałbym wyjaśnić Ci, czym jest tzw. "okrąg jednostkowy". Jeśli pamiętasz jeszcze cokolwiek ze szkolnej matematyki ("Nie śpij na mnie!") to okrąg ma promień. Promień okręgu jest odległością ze środka okręgu do krawędzi. Okrąg jednostkowy to taki, którego promień wynosi dokładnie 1.

To jest okrąg jednostkowy:

Zauważ, że gdy ciągniesz za niebieski "uchwyt" na okręgu, to jego pozycja X i Y zmienia się. Współrzędne reprezentują położenie punktu na okręgu. Na górze Y wynosi 1, a X jest 0. Po prawej stronie X wynosi 1, a Y jest 0.

Jeśli pamiętasz podstawy matematyki to mnożenie czegoś przez 1 pozostawia to coś niezmienione. Zatem 123 * 1 = 123. Proste, prawda? A więc dobrze. Okrąg jednostkowy o promieniu 1 jest także pewną formą jedynki. On jest taką "obracającą jedynką". Tzn. możesz pomnożyć coś przez okrąg jednostkowy i to zachowa się w sposób podobny do mnożenia przez 1 z dokładnością do tego, że rzeczy się obracają.

Będziemy mnożyć przez współrzędne X i Y punktu na okręgu jednostkowym geometrię z naszego poprzedniego przykładu.

Poniżej są aktualizacje wymagane dla naszego cieniowania.

<script id="vertex-shader-2d" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;

void main() {
  // Obróć pozycję:
  vec2 rotatedPosition = vec2(
     a_position.x * u_rotation.y + a_position.y * u_rotation.x,
     a_position.y * u_rotation.y - a_position.x * u_rotation.x);

  // Dodaj przesunięcie:
  vec2 position = rotatedPosition + u_translation;

Aktualizujemy również JavaScript, żebyśmy mogli przekazać te dwie wartości.

  ...
  var rotationLocation = gl.getUniformLocation(program, "u_rotation");
  ...
  var rotation = [0, 1];
  ..
  // Narysuj scenę.
  function drawScene() {
    // Wyczyść płótno.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Ustaw przesunięcie.
    gl.uniform2fv(translationLocation, translation);

    // Ustaw obrót.
    gl.uniform2fv(rotationLocation, rotation);

    // Narysuj prostokąt.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Oto rezultat. Przeciągaj uchwyt po okręgu w celu obrotu lub suwaki w celu przesunięcia.

Dlaczego to działa? Spójrz na te wzory.

rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;

Załóżmy, że masz prostokąt i chcesz go obracać. Zanim zaczniesz nim kręcić jego górny, prawy wierzchołek jest na pozycji 3.0, 9.0. Wybierzmy punkt na okręgu jednostkowym - 30 stopni zgodnie z ruchem wskazówek zegara od godziny 12.

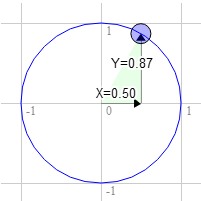
Pozycja na okręgu wynosi wtedy 0.50 i 0.87:

   3.0 * 0.87 + 9.0 * 0.50 = 7.1
   9.0 * 0.87 - 3.0 * 0.50 = 6.3

To jest dokładnie tam gdzie chcemy, żeby był:

Tak samo dla 60 stopni w kierunku ruchu wskazówek zegara:

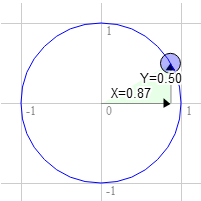
Pozycja na okręgu wynosi wtedy 0.87 i 0.50:

   3.0 * 0.50 + 9.0 * 0.87 = 9.3
   9.0 * 0.50 - 3.0 * 0.87 = 1.9

Przesuwając punkt po okręgu zgodnie z ruchem wskazówek zegara, możesz zobaczyć, że wartości X stają się większe, a wartości Y mniejsze, Gdy przekraczasz 90 stopni wartości X zaczynają się zmniejszać, a wartości Y stają się ujemne... Tak wyłania się wzorzec objawiający się jako obrót.

Istnieje specjalna nazwa dla współrzędnych punktów z okręgu jednostkowego - sinus i cosinus. Tak więc dla dowolnego zadanego kąta możemy odszukać sinus i cosinus, jak poniżej:

function printSineAndCosineForAnAngle(angleInDegrees) {
  var angleInRadians = angleInDegrees * Math.PI / 180;
  var s = Math.sin(angleInRadians);
  var c = Math.cos(angleInRadians);
  console.log("s = " + s + " c = " + c);
}

Jeśli skopiujesz powyższy kod i wkleisz do konsoli JavaScript, a następnie wywołasz funkcję printSineAndCosignForAngle(30) zobaczysz, że to wypisze s = 0.49 c= 0.87 (zauważ, że zaokrągliłem liczby.)

Łącząc to wszystko w całość możesz obracać swoją geometrię o dowolny kąt jakiego potrzebujesz. Po prostu podajesz jako argument funkcji sinus i cosinus kąt o jaki chcesz obrócić.

  ...
  var angleInRadians = angleInDegrees * Math.PI / 180;
  rotation[0] = Math.sin(angleInRadians);
  rotation[1] = Math.cos(angleInRadians);

Oto wersja, która ustawia kąt - przeciągaj suwaki, aby przesuwać i obracać.

Mam nadzieję, że to ma sens. Następny temat jest prostszy. Skalowanie.